6.6 Bilinear Patches
It is useful to have a shape defined by four vertices. One option would be a planar quadrilateral, though not requiring all four vertices to be coplanar is preferable, as it is less restrictive. Such a shape is the bilinear patch, which is a parametric surface defined by four vertices , , , and . Each vertex gives the position associated with a corner of the parametric domain and points on the surface are defined via bilinear interpolation:
The bilinear patch is a doubly ruled surface: there are two straight lines through every point on it. (This can be seen by considering a parametric point on the surface and then fixing either of and and considering the function that results: it is linear.)
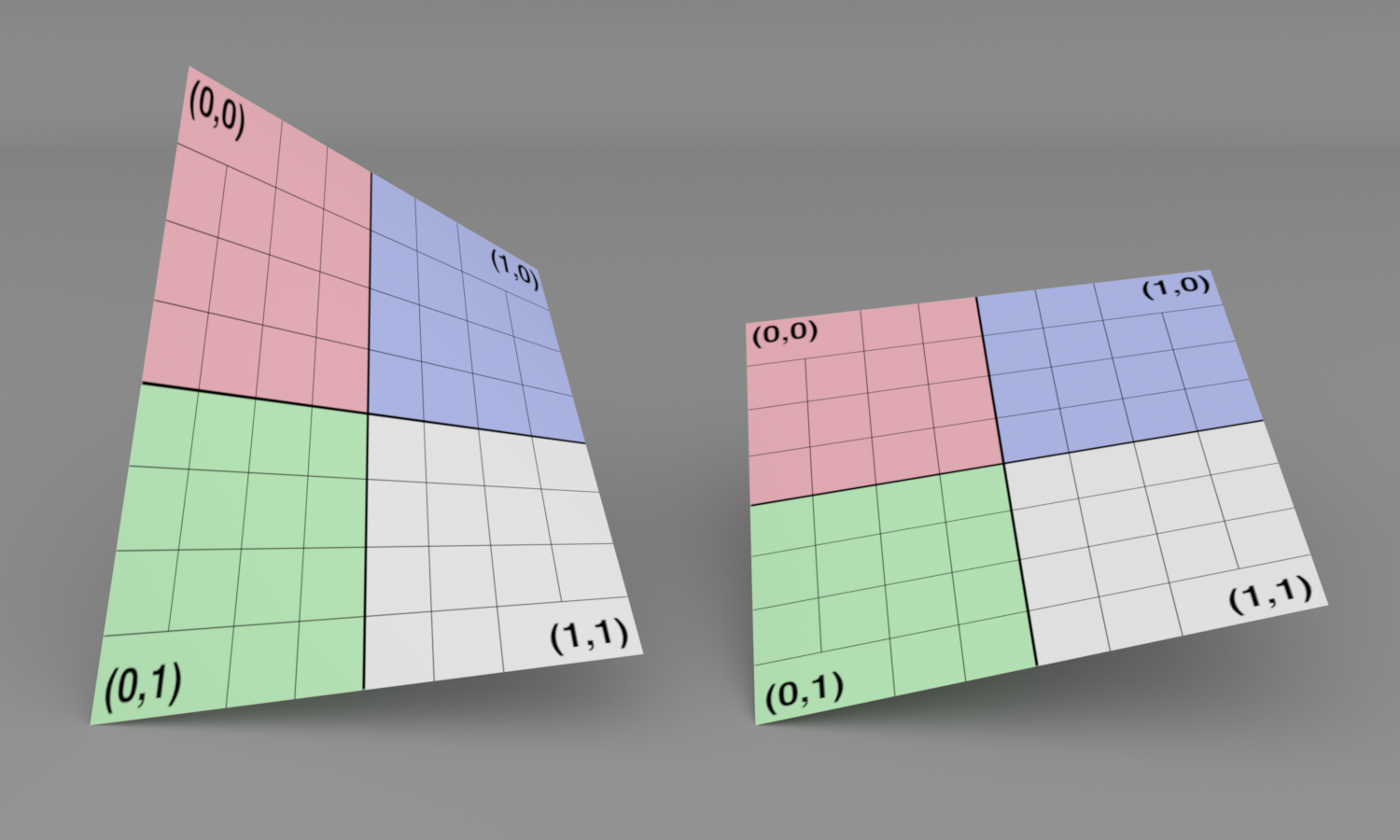
Not only can bilinear patches be used to represent planar quadrilaterals, but they can also represent simple curved surfaces. They are a useful target for converting higher-order parametric surfaces to simpler shapes that are amenable to direct ray intersection. Figure 6.22 shows two bilinear patches.
pbrt allows the specification of bilinear patch meshes for the same reasons that triangle meshes can be specified: to allow per-vertex attributes like position and surface normal to be shared by multiple patches and to allow mesh-wide properties to be stored just once. To this end, BilinearPatchMesh plays the equivalent role to the TriangleMesh.
We will skip past the BilinearPatchMesh constructor, as it mirrors the TriangleMesh’s, transforming the positions and normals to rendering space and using the BufferCache to avoid storing redundant buffers in memory.
The BilinearPatch class implements the Shape interface and represents a single patch in a bilinear patch mesh.
Also similar to triangles, each BilinearPatch stores the index of the mesh that it is a part of as well as its own index in the mesh’s patches.
The GetMesh() method makes it easy for a BilinearPatch to get the pointer to its associated mesh.
There is a subtlety that comes with the use of a vector to store the meshes. pbrt’s scene initialization code in Appendix C does its best to parallelize its work, which includes the parallelization of reading binary files that encode meshes from disk. A mutex is used to protect adding meshes to this vector, though as this vector grows, it is periodically reallocated to make more space. A consequence is that the BilinearPatch constructor must not call the GetMesh() method to get its BilinearPatchMesh *, since GetMesh() accesses allMeshes without mutual exclusion. Thus, the mesh is passed to the constructor as a parameter above.
The area of a parametric surface defined over is given by the integral
The partial derivatives of a bilinear patch are easily derived. They are:
However, it is not generally possible to evaluate the area integral from Equation (6.12) in closed form with these partial derivatives. Therefore, the BilinearPatch constructor caches the patch’s surface area in a member variable, using numerical integration to compute its value if necessary.
Because bilinear patches are often used to represent rectangles, the constructor checks for that case and takes the product of the lengths of the sides of the rectangle to compute the area when appropriate. In the general case, the fragment <<Compute approximate area of bilinear patch>> uses a Riemann sum evaluated at points to approximate Equation (6.12). We do not include that code fragment here.
This fragment, which loads the four vertices of a patch into local variables, will be reused in many of the following methods.
In addition to the surface area computation, there will be a number of additional cases where we will find it useful to use specialized algorithms if a BilinearPatch is a rectangle. Therefore, this check is encapsulated in the IsRectangle() method.
It first tests to see if any two neighboring vertices are coincident, in which case the patch is certainly not a rectangle. This check is important to perform first, since the following ones would otherwise end up trying to perform invalid operations like normalizing degenerate vectors in that case.
If the four vertices are not coplanar, then they do not form a rectangle. We can check this case by computing the surface normal of the plane formed by three of the vertices and then testing if the vector from one of those three to the fourth vertex is not (nearly) perpendicular to the plane normal.
Four coplanar vertices form a rectangle if they all have the same distance from the average of their positions. The implementation here computes the squared distance to save the square root operations and then tests the relative error with respect to the first squared distance. Because the test is based on relative error, it is not sensitive to the absolute size of the patch; scaling all the vertex positions does not affect it.
With the area cached, implementation of the Area() method is trivial.
The bounds of a bilinear patch are given by the bounding box that bounds its four corner vertices. As with Triangles, the mesh vertices are already in rendering space, so no further transformation is necessary here.
Although a planar patch has a single surface normal, the surface normal of a nonplanar patch varies across its surface.
If the bilinear patch is actually a triangle, the <<If patch is a triangle, return bounds for single surface normal>> fragment evaluates its surface normal and returns the corresponding DirectionCone. We have not included that straightforward fragment here.
Otherwise, the normals are computed at the four corners of the patch. The following fragment computes the normal at the parametric position. It is particularly easy to evaluate the partial derivatives at the corners; they work out to be the differences with the adjacent vertices in and . Some care is necessary with the orientation of the normals, however. As with triangle meshes, if per-vertex shading normals were specified, they determine which side of the surface the geometric normal lies on. Otherwise, the normal may need to be flipped, depending on the user-specified orientation and the handedness of the rendering-to-object-space transformation.
Normals at the other three vertices are computed in an equivalent manner, so the fragment that handles the rest is not included here.
A bounding cone for the normals is found by taking their average and then finding the cosine of the maximum angle that any of them makes with their average. Although this does not necessarily give an optimal bound, it usually works well in practice. (See the “Further Reading” section in Chapter 3 for more information on this topic.)
6.6.1 Intersection Tests
Unlike triangles (but like spheres and cylinders), a ray may intersect a bilinear patch twice, in which case the closest of the two intersections is returned. An example is shown in Figure 6.23.
As with triangles, it is useful to have a stand-alone ray–bilinear patch intersection test function rather than only providing this functionality through an instance of a BilinearPatch object. Rather than being based on computing values along the ray and then finding the coordinates for any found intersections, the algorithm here first determines the parametric coordinates of any intersections. Only if any are found within are the corresponding and values computed to find the full intersection information.
Going back to the definition of the bilinear surface, Equation (6.11), we can see that if we fix one of or , then we are left with an equation that defines a line. For example, with fixed, we have
with
(See Figure 6.24.)
The first step of the intersection test considers the set of all such lines defined by the patch’s vertices. For any intersection, the minimum distance from a point along the ray to a point along one of these lines will be zero. Therefore, we start with the task of trying to find values that give lines with zero distance to a point on the ray.
Given two infinite and non-parallel lines, one defined by the two points and and the other defined by and , the minimum distance between them can be found by determining the pair of parallel planes that each contain one of the lines and then finding the distance between them. (See Figure 6.25.)
To find the coefficients of those plane equations, we start by taking the cross product . This gives a vector that is perpendicular to both lines and provides the first three coefficients of the plane equation . In turn, the and coefficients can be found for each line’s plane by substituting a point along the respective line into the plane equation and solving for . Because the planes are parallel, the distance between them is then
In the case of ray–bilinear patch intersection, one line corresponds to the ray and the other to a line from the family of lines given by .
Given a ray and the bilinear patch vertices, we have , the ray’s origin, and can be set as the point along the ray . Then, and can be set as and from Equation (6.14). After taking the cross product to find the plane coefficients, finding each value, and simplifying, we can find that is a quadratic equation in . (That it is quadratic is reassuring, since a ray can intersect a bilinear patch up to two times.)
Because we only care about finding zeros of the distance function, we can neglect the denominator of Equation (6.15). After equating the difference to 0, collecting terms and simplifying, we end up with the following code to compute the quadratic coefficients.
The values where the ray intersects the patch are given by the solution to the corresponding quadratic equation. If there are no real solutions, then there is no intersection and the function returns.
The two values are handled in turn. The first step is to check whether each is between 0 and 1. If not, it does not represent a valid intersection in the patch’s parametric domain. Otherwise, the and values for the intersection point are computed.
One way to compute the and values is to find the parametric values along the ray and the line where the distance between them is minimized. Although this distance should be zero since we have determined that there is an intersection between the ray and , there may be some round-off error in the computed u value. Thus, formulating this computation in terms of minimizing that distance is a reasonable way to make the most of the values at hand.
With the ray’s origin and its direction, the parameter values where the distances are minimized are given by
and
where is shorthand for the determinant of the matrix formed from the three column vectors. We will not derive these equations here. The “Further Reading” section has more details.
We start by computing a handful of common values that are used in computing the matrix determinants and final parametric values.
The matrix determinants in the numerators can easily be computed using the SquareMatrix class. Note that there are some common subexpressions among the two of them, though we leave it to the compiler to handle them. In a more optimized implementation, writing out the determinant computations explicitly in order to do so manually could be worthwhile.
Due to round-off error, it is possible that the computed distance is positive and seemingly represents a valid intersection even though the true value of is negative and corresponds to a point behind the ray’s origin. Testing against an epsilon value (which is discussed further in Section 6.8.7) helps avoid reporting incorrect intersections in such cases. Because we defer the division to compute the final value, it is necessary to test t1 against p2 * eps here.
The second root is handled with equivalent code, though with added logic to keep the closer of the intersections if there are two of them. That fragment is not included here.
If the final closest value is less than the given tMax, then an intersection is returned.
The coordinates and ray parametric value are sufficient to encapsulate the intersection so that the rest of its geometric properties can be computed later.
The InteractionFromIntersection() method computes all the geometric information necessary to return the SurfaceInteraction corresponding to a specified point on a bilinear patch, as is found by the intersection routine.
Given the parametric coordinates of an intersection point, it is easy to compute the corresponding point on the bilinear patch using Equation (6.11) and its partial derivatives with Equation (6.13).
If per-vertex texture coordinates have been specified, then they, too, are interpolated at the intersection point. Otherwise, the parametric coordinates are used for texture mapping. For the remainder of this method, we will denote the texture coordinates as to distinguish them from the patch’s parameterization. (Because this method does not use the parametric distance along the ray, this notation is unambiguous.)
Variables are also defined here to store the partial derivatives between the two sets of coordinates: , , , and . These are initialized for now to the appropriate values for when .
If per-vertex texture coordinates have been specified, they are bilinearly interpolated in the usual manner.
Because the partial derivatives and in the SurfaceInteraction are in terms of the parameterization used for texturing, these values must be updated if texture coordinates have been specified.
The first step is to compute the updated partial derivatives and so forth. These can be found by first taking the corresponding partial derivatives of the bilinear interpolation used to compute to find and . (Note the similar form to how the partial derivatives of were computed earlier.) The desired partial derivatives can be found by taking reciprocals.
Given the partial derivatives, the chain rule can be applied to compute the updated partial derivatives of position. For example,
and similarly for .
If the provided texture coordinates specify a degenerate mapping, or may be zero. In that case, dpdu and dpdv are left unchanged, as at least their cross product provides a correct normal vector. A dot product checks that the normal given by lies in the same hemisphere as the normal given by the cross product of the original partial derivatives of , flipping if necessary. Finally, dpdu and dpdv can be updated.
The second partial derivatives of are easily found to compute the partial derivatives of the surface normal; all but are zero vectors. Thence, the partial derivatives of the normal can be computed using the regular approach. These are then adjusted to account for the parameterization in the same way that and were. The corresponding fragment follows the same form as <<Compute partial derivatives of with respect to >> and is therefore not included here.
All the necessary information for initializing the SurfaceInteraction is now at hand.
Shading geometry is set in the SurfaceInteraction after it is created. Therefore, per-vertex shading normals are handled next.
The usual bilinear interpolation is performed and if the resulting normal is non-degenerate, the shading geometry is provided to the SurfaceInteraction.
The partial derivatives of the shading normal are computed in the same manner as the partial derivatives of were found, including the adjustment for the parameterization given by per-vertex texture coordinates, if provided. Because shading geometry is specified via shading and vectors, here we find the rotation matrix that takes the geometric normal to the shading normal and apply it to dpdu and dpdv. The cross product of the resulting vectors then gives the shading normal.
Given the intersection and InteractionFromIntersection() methods, both of the BilinearPatch::Intersect() and IntersectP() methods are easy to implement. Since they both follow what should be by now a familiar form, we have not included them here.
6.6.2 Sampling
The sampling routines for bilinear patches select between sampling algorithms depending on the characteristics of the patch. For area sampling, both rectangular patches and patches that have an emission distribution defined by an image map are given special treatment. When sampling by solid angle from a reference point, rectangular patches are projected on to the sphere and sampled as spherical rectangles. For both cases, general-purpose sampling routines are used otherwise.
The area sampling method first samples parametric coordinates, from which the rest of the necessary geometric values are derived.
While all the Shape implementations we have implemented so far can be used as area light sources, none of their sampling routines have accounted for the fact that pbrt’s DiffuseAreaLight allows specifying an image that is used to represent spatially varying emission over the shape’s surface. Because such emission profiles are most frequently used with rectangular light sources, the BilinearPatch has the capability of sampling in according to the emission function. Figure 6.26 demonstrates the value of doing so.
Otherwise, if the patch is not a rectangle, an approximation to uniform area sampling is used. If it is a rectangle, then uniform area sampling is trivial and the provided sample value is used directly for . In all of these cases, the pdf value is with respect to the parametric domain over .
For patches without an emissive image to sample from, we would like to uniformly sample over their surface area, as we have done with all the shapes so far. Unfortunately, an exact equal-area sampling algorithm cannot be derived for bilinear patches. This is a consequence of the fact that it is not possible to integrate the expression that gives the area of a bilinear patch, Equation (6.12). It is easy to uniformly sample in parametric space, but doing so can give a poor distribution of samples, especially for bilinear patches where two vertices are close together and the others are far apart. Figure 6.27 shows such a patch as well as the distribution of points that results from uniform parametric sampling. While the nonuniform distribution of points can be accounted for in the PDF such that Monte Carlo estimates using such samples still converge to the correct result, the resulting estimators will generally have higher error than if a more uniform distribution is used.
An exact equal-area sampling algorithm would sample points with probability proportional to its differential surface area . Lacking the ability to sample directly from this distribution, we will approximate it with a bilinear function where the value of the function at each corner is given by the patch’s differential surface area there. Sampling a location from that distribution generally works well to approximate exact equal-area sampling; see Figure 6.28.
It is especially easy to compute the partial derivatives at the patch corners; they are just differences with the adjacent vertices.
Given a position on the patch, the corresponding position, partial derivatives, and surface normal can all be computed, following the same approach as was implemented in InteractionFromIntersection(). The fragment <<Compute , , and for sampled >> is therefore not included here, and texture coordinates for the sampled point are computed using a fragment defined earlier.
Only the geometric normal is needed for sampled points. It is easily found via the cross product of partial derivatives of the position. The <<Flip normal at sampled if necessary>> fragment negates the normal if necessary, depending on the mesh properties and shading normals, if present. It follows the same form as earlier fragments that orient the geometric normal based on the shading normal, if present, and otherwise the reverseOrientation and transformSwapsHandedness properties of the mesh.
The PDF value stored in pdf gives the probability of sampling the position uv in parametric space. In order to return a PDF defined with respect to the patch’s surface area, it is necessary to account for the corresponding change of variables, which results in an additional factor of .
The PDF for sampling a given point on a bilinear patch is found by first computing the probability density for sampling its position in parametric space and then transforming that density to be with respect to the patch’s surface area.
If coordinates have been specified at the vertices of a bilinear patch, then the member variable Interaction::uv stores interpolated texture coordinates. In the following, we will need the parametric coordinates over the patch’s domain, which can be found via a call to InvertBilinear().
Regardless of which sampling technique is used for a bilinear patch, finding the PDF for a sample is straightforward.
The partial derivatives are computed from as they have been before and so we omit the corresponding fragment. Given dpdu and dpdv, the same scaling factor as was used in Sample() is used to transform the PDF.
The solid angle sampling method handles general bilinear patches with the same approach that was used for Cylinders and Disks: a sample is taken with respect to surface area on the surface using the first sampling method and is returned with a probability density expressed in terms of solid angle. Rectangular patches are handled using a specialized sampling technique that gives better results.
If the patch is not a rectangle, is very small, or has a sampling distribution associated with it to match textured emission, then the regular area sampling method is used and the PDF with respect to area is converted to be with respect to solid angle. Otherwise, a specialized solid angle sampling technique is used.
Rectangular patches are projected on the sphere to form a spherical rectangle that can then be sampled directly. Doing so gives similar benefits to sampling spherical triangles, as was implemented in Section 6.5.4.
Also as with triangles, we incorporate an approximation to the factor at the reference point by warping the uniform sample u using a bilinear approximation to the function in the sampling space.
The spherical rectangle sampling algorithm maintains the relationship between each corner of the sampling space and the corresponding corner of the patch in its parametric space. Therefore, each bilinear sampling weight is set using the factor to the corresponding vertex of the patch.
In addition to the sample u, SampleSphericalRectangle() takes a reference point, the corner of the rectangle, and two vectors that define its edges. It returns a point on the patch and the sampling PDF, which is one over the solid angle that it subtends.
The implementation of the SampleSphericalRectangle() function is another interesting exercise in spherical trigonometry, like SampleSphericalTriangle() was. However, in the interests of space, we will not include discussion of its implementation here; the “Further Reading” section has a pointer to the paper that introduced the approach and describes its derivation.
A rectangle has the same surface normal across its entire surface, which can be found by taking the cross product of the two edge vectors. The parametric coordinates for the point p are then found by computing the normalized projection of p onto each of the edges.
If the bilinear patch has per-vertex texture coordinates associated with it, the interpolated texture coordinates at the sampled point are easily computed.
The associated PDF() method follows the usual form, determining which sampling method would be used for the patch and then computing its solid angle PDF.
In all cases, the SurfaceInteraction corresponding to the intersection of the ray from ctx in the direction wi will be needed, so the method starts by performing a ray–patch intersection test.
If one of the area sampling approaches was used, then a call to the other PDF() method provides the PDF with respect to surface area, which is converted to be with respect to solid angle before it is returned.
Otherwise, the spherical rectangle sampling technique was used. The uniform solid angle PDF is 1 over the solid angle that the rectangle subtends. If the reference point is on a surface and the approximation to the factor would be applied in the Sample() method, then the PDF for sampling u must be included as well.
The InvertSphericalRectangleSample() function, not included here, returns the sample value u that maps to the given point pRect on the rectangle when the SampleSphericalRectangle() is called with the given reference point pRef.