B.2 Mathematical Infrastructure
pbrt uses a wide range of mathematical routines. Much of this functionality is implemented in the files util/math.h and util/math.cpp; everything in this section is found there, with a few exceptions that will be noted when they are encountered.
A table of the first 1,000 prime numbers is provided via a global variable. Its main use in pbrt is for determining bases to use for the radical inverse based low-discrepancy points in Chapter 8.
NextPrime() returns the next prime number after the provided one.
B.2.1 Basic Algebraic Functions
Clamp() clamps the given value to lie between the values low and high. For convenience, it allows the types of the values giving the extent to be different than the type being clamped (but its implementation requires that implicit conversion among the types involved is legal). By being implemented this way rather than requiring all to have the same type, the implementation allows calls like Clamp(floatValue, 0, 1) that would otherwise be disallowed by C++’s template type resolution rules.
Mod() computes the remainder of . pbrt has its own version of this (rather than using %) in order to provide the behavior that the modulus of a negative number is always positive or zero. Starting with C++11, the behavior of % has been specified to return a negative value or zero in this case, so that the identity (a/b)*b + a%b == a holds.
A specialization for Floats calls the corresponding standard library function.
It can be useful to be able to invert the bilinear interpolation function, Equation (2.25). Because there are two unknowns in the result, values with at least two dimensions must be bilinearly interpolated in order to invert it. In that case, two equations with two unknowns can be formed, which in turn leads to a quadratic equation.
A number of constants, most of them related to , are used enough that it is worth having them easily available.
Two simple functions convert from angles expressed in degrees to radians, and vice versa:
It is often useful to blend between two values using a smooth curve that does not have the first derivative discontinuities that a linear interpolant would. SmoothStep() takes a range and a value , returning 0 if , 1 if , and smoothly blends between 0 and 1 for intermediate values of using a cubic polynomial. Among other uses in the system, the SpotLight uses SmoothStep() to model the falloff to its edge.
Finally, SafeSqrt() returns the square root of the given value, clamping it to zero in case of rounding errors being the cause of a slightly negative value. A second variant for doubles is effectively the same and is therefore not included here.
B.2.2 Integer Powers and Polynomials
Sqr() squares the provided value. Though it is not much work to write this operation out directly, we have often found this function to be helpful in making the implementations of formulae more succinct.
Pow() efficiently raises a value to a power if the power is a compile-time constant. Note that the total number of multiply operations works out to be logarithmic in the power n.
Specializations for and terminate the template function recursion.
EvaluatePolynomial() evaluates a provided polynomial using Horner’s method, which is based on the equivalence
This formulation both gives good numerical accuracy and is amenable to use of fused multiply add operations.
B.2.3 Trigonometric Functions
The function is used in multiple places in pbrt, including in the implementation of the LanczosSincFilter. It is undefined at and suffers from poor numerical accuracy if directly evaluated at nearby values. A robust computation of its value is possible by considering the power series expansion
If is small and rounds to 1, then also rounds to 1. The following function uses a slightly more conservative variant of that test, which is close enough for our purposes.
Similar to SafeSqrt(), pbrt also provides “safe” versions of the inverse sine and cosine functions so that if the provided value is slightly outside of the legal range , a reasonable result is returned rather than a not-a-number value. In debug builds, an additional check is performed to make sure that the provided value is not too far outside the valid range.
B.2.4 Logarithms and Exponentiation
Because the math library does not provide a base-2 logarithm function, we provide one here, using the identity .
If only the integer component of the base-2 logarithm of a float is needed, then the result is available (nearly) in the exponent of the floating-point representation. In the implementation below, we augment that approach by testing the significand of the provided value to the midpoint of significand values between the current exponent and the next one up, using the result to determine whether rounding the exponent up or rounding it down gives a more accurate result. A corresponding function for doubles is not included here.
It is also often useful to be able to compute the base-2 logarithm of an integer. Rather than computing an expensive floating-point logarithm and converting to an integer, it is much more efficient to count the number of leading zeros up to the first one in the 32-bit binary representation of the value and then subtract this value from 31, which gives the index of the first bit set, which is in turn the integer base-2 logarithm. (This efficiency comes in part from the fact that most processors have an instruction to count these zeros.)
Though we generally eschew including target-specific code in the book text, we will make an exception here just as an illustration of the messiness that often results when it is necessary to leave the capabilities of the standard libraries to access features that have different interfaces on different targets.
It is occasionally useful to compute the base-4 logarithm of an integer value. This is easily done using the identity .
An efficient approximation to the exponential function comes in handy, especially for volumetric light transport algorithms where such values need to be computed frequently. Like Log2Int(), this value can be computed efficiently by taking advantage of the floating-point representation.
The first step is to convert the problem into one to compute a base-2 exponential; a factor of does so. This step makes it possible to take advantage of computers’ native floating-point representation.
Next, the function splits the exponent into an integer and a fractional part , giving .
Because is between 0 and 1, can be accurately approximated with a polynomial. We have fit a cubic polynomial to this function using a constant term of 1 so that is exact. The following coefficients give a maximum absolute error of less than over the range of .
The last task is to apply the scale. This can be done by directly operating on the exponent in the twoToF value. It is necessary to make sure that the resulting exponent fits in the valid exponent range of 32-bit floats; if it does not, then the computation has either underflowed to 0 or overflowed to infinity. If the exponent is valid, then the existing exponent bits are cleared so that final exponent can be stored. (For the source of the value of 127 that is added to the exponent, see Equation (6.17).)
The integral of the Gaussian over a range can be expressed in terms of the error function, which is available from the standard library.
The logistic distribution takes a scale factor , which controls its width:
It has a generally similar shape to the Gaussian—it is symmetric and smoothly falls off from its peak—but it can be integrated in closed form. Evaluating the logistic is straightforward, though it is worth taking the absolute value of to avoid numerical instability for when the ratio is relatively large. (The function is symmetric around the origin, so this is mathematically equivalent.)
The logistic function is normalized so it is its own probability density function (PDF). Its cumulative distribution function (CDF) can be easily found via integration.
The trimmed logistic function is the logistic limited to an interval and then renormalized using the technique introduced in Section A.4.5.
ErfInv() is the inverse to the error function std:erf(), implemented via a polynomial approximation. I0() evaluates the modified Bessel function of the first kind and LogI0() returns its logarithm.
B.2.6 Interval Search
FindInterval() is a helper function that emulates the behavior of std::upper_bound() but uses a function object to get values at various indices instead of requiring access to an actual array. This way, it becomes possible to bisect arrays that are procedurally generated, such as those interpolated from point samples.
It generally returns the index such that is true and is false. However, since this function is primarily used to locate an interval for linear interpolation, it applies the following boundary conditions to prevent out-of-bounds accesses and to deal with predicates that evaluate to true or false over the entire domain:
- The returned index is no larger than sz-2, so that it is always legal to access both of the elements and .
- If there is no index such that the predicate is true, 0 is returned.
- If there is no index such that the predicate is false, sz-2 is returned.
B.2.7 Bit Operations
There are clever tricks that can be used to efficiently determine if a given integer is an exact power of 2, or round an integer up to the next higher (or equal) power of 2. (It is worthwhile to take a minute and work through for yourself how these two functions work.)
A variant of RoundUpPow2() for int64_t is also provided but is not included in the text here.
The bits of an integer quantity can be efficiently reversed with a series of bitwise operations. The first line of the ReverseBits32() function, which reverses the bits of a 32-bit integer, swaps the lower 16 bits with the upper 16 bits of the value. The next line simultaneously swaps the first 8 bits of the result with the second 8 bits and the third 8 bits with the fourth. This process continues until the last line, which swaps adjacent bits. To understand this code, it is helpful to write out the binary values of the various hexadecimal constants. For example, 0xff00ff00 is 11111111000000001111111100000000 in binary; it is then easy to see that a bitwise or with this value masks off the first and third 8-bit quantities.
The bits of a 64-bit value can then be reversed by reversing the two 32-bit components individually and then interchanging them.
Morton Indexing
To be able to compute 3D Morton codes, which were introduced in Section 7.3.3, we will first define a helper function: LeftShift3() takes a 32-bit value and returns the result of shifting the th bit to be at the th bit, leaving zeros in other bits. Figure B.1 illustrates this operation.
The most obvious approach to implement this operation, shifting each bit value individually, is not the most efficient. (It would require a total of 9 shifts, along with bitwise or operations to compute the final value.) Instead, we can decompose each bit’s shift into multiple shifts of power-of-two size that together shift the bit’s value to its final position. Then, all the bits that need to be shifted a given power-of-two number of places can be shifted together. The LeftShift3() function implements this computation, and Figure B.2 shows how it works.
EncodeMorton3() takes a 3D coordinate value where each component is a floating-point value between 0 and . It converts these values to integers and then computes the Morton code by expanding the three 10-bit quantized values so that their th bits are at position , then shifting the bits over one more, the bits over two more, and computing the bitwise or of the result (Figure B.3).
Support for 2D Morton encoding is provided by the EncodeMorton2() function, which takes a pair of 32-bit integer values and follows an analogous approach. It is not included here.
B.2.8 Hashing and Random Permutations
A handful of hashing functions are provided. Their implementations are in the file [EntityList: util/cmd: -: hash.h].
The first, MixBits(), takes an integer value and applies a so-called finalizer, which is commonly found at the end of hash function implementations. A good hash function has the property that flipping a single bit in the input causes each of the bits in the result to flip with probability ; a finalizer takes values where this may not be the case and shuffles them around in a way that increases this likelihood.
MixBits() is particularly handy for tasks like computing unique seeds for a pseudo-random number generator at each pixel: depending on the RNG implementation, the naive approach of converting the pixel coordinates into an index and giving the RNG successive integer values as seeds may lead to correlation between values it generates at nearby pixels. Running such an index through MixBits() first is good protection against this.
There are also complete hash functions for arbitrary data. HashBuffer() hashes a region of memory of given size using MurmurHash64A, which is an efficient and high-quality hash function.
For convenience, pbrt also provides a Hash() function that can be passed an arbitrary sequence of values, all of which are hashed together.
It is sometimes useful to convert a hash to a floating-point value between 0 and 1; the HashFloat() function handles the details of doing so.
PermutationElement() returns the ith element of a random permutation of n values based on the provided seed. Remarkably, it is able to do so without needing to explicitly represent the permutation. The key idea underlying its implementation is the insight that any invertible hash function of bits represents a permutation of the values from 0 to —otherwise, it would not be invertible.
Such a hash function can be used to define a permutation over a non-power-of-two number of elements using the permutation for the next power-of-two number of elements and then repermuting any values greater than until a valid one is reached.
B.2.9 Error-Free Transformations
It is possible to increase the accuracy of some floating-point calculations using an approach known as error-free transformations (EFT). The idea of them is to maintain the accumulated error that is in a computed floating-point value and to then make use of that error to correct later computations. For example, we know that the rounded floating-point value is in general not equal to the true product . Using EFTs, we also compute an error term such that
A clever use of fused multiply add (FMA) makes it possible to compute without resorting to higher-precision floating-point numbers. Consider the computation FMA(-a, b, a * b): on the face of it, it computes zero, adding the negated product of and to itself. In the context of the FMA operation, however, it gives the rounding error, since the product of and is not rounded before , which is rounded, is added to it.
TwoProd() multiplies two numbers and determines the error, returning both results using the CompensatedFloat structure.
CompensatedFloat is a small wrapper class that holds the results of EFT-based computations.
It provides the expected constructor and conversion operators, which are qualified with explicit to force callers to express their intent to use them.
It is also possible to compute a compensation term for floating-point addition of two values: .
It is not in general possible to compute exact compensation terms for sums or products of more than two values. However, maintaining them anyway, even if they carry some rounding error, makes it possible to implement various algorithms with lower error than if they were not used.
A similar trick based on FMA can be applied to the difference-of-products calculation of the form . To understand the challenge involved in this computation, consider computing this difference as . There are two rounding operations, one after computing and then another after the FMA. If, for example, all of , , , and are positive and the products and are of similar magnitudes, then catastrophic cancellation may result: the rounding error from , though small with respect to the product , may be large with respect to the final result.
The following DifferenceOfProducts() function uses FMA in a similar manner to TwoProd(), finding an initial value for the difference of products as well as the rounding error from . The rounding error is then added back to the value that is returned, thus fixing up catastrophic cancellation after the fact. It has been shown that this gives a result within 1.5 ulps of the correct value; see the “Further Reading” section for details.
pbrt also provides a SumOfProducts() function that reliably computes in a similar manner.
Compensation can also be used to compute a sum of numbers more accurately than adding them together directly. An algorithm to do so is implemented in the CompensatedSum class.
The value added to the sum, delta, is the difference between the value provided and the accumulated error in c. After the addition is performed, the compensation term is updated appropriately.
B.2.10 Finding Zeros
The Quadratic() function finds solutions of the quadratic equation ; the Boolean return value indicates whether solutions were found.
If a is zero, then the caller has actually specified a linear function. That case is handled first to avoid not-a-number values being generated via the usual execution path. (Our implementation does not handle the case of all coefficients being equal to zero, in which case there are an infinite number of solutions.)
The discriminant is computed using DifferenceOfProducts(), which improves the accuracy of the computed value compared to computing it directly using floating-point multiplication and subtraction. If the discriminant is negative, then there are no real roots and the function returns false.
The usual version of the quadratic equation can give poor numerical accuracy when due to cancellation error. It can be rewritten algebraically into a more stable form:
where
The implementation uses pstd::copysign() in place of an if test for the condition on , setting the sign of the square root of the discriminant to be the same as the sign of , which is equivalent. This micro-optimization does not meaningfully affect pbrt’s performance, but it is a trick that is worth being aware of.
NewtonBisection() finds a zero of an arbitrary function over a specified range using an iterative root-finding technique that is guaranteed to converge to the solution so long as brackets a root and and differ in sign.
In each iteration, bisection search splits the interval into two parts and discards the subinterval that does not bracket the solution—in this way, it can be interpreted as a continuous extension of binary search. The method’s robustness is clearly desirable, but its relatively slow (linear) convergence can still be improved. We therefore use Newton-bisection, which is a combination of the quadratically converging but potentially unsafe Newton’s method with the safety of bisection search as a fallback.
The provided function f should return a std::pair<Float, Float> where the first value is the function’s value and the second is its derivative. Two “epsilon” values control the accuracy of the result: xEps gives a minimum distance between the values that bracket the root, and fEps specifies how close to zero is sufficient for .
Before the iteration begins, a check is performed to see if one of the endpoints is a zero. (For example, this case comes up if a zero-valued function is specified.) If so, there is no need to do any further work.
The number of required Newton-bisection iterations can be reduced by starting the algorithm with a good initial guess. The function uses a heuristic that assumes that the function is linear and finds the zero crossing of the line between the two endpoints.
The first fragment in the inner loop checks if the current proposed midpoint is inside the bracketing interval . Otherwise, it is reset to the interval center, resulting in a standard bisection step (Figure B.4).
The function can now be evaluated and the bracket range can be refined. Either x0 or x1 is set to xMid in a way that maintains the invariant that the function has different signs at and .
The iteration stops either if the function value is close to 0 or if the bracketing interval has become sufficiently small.
If the iteration is to continue, an updated midpoint is computed using a Newton step. The next loop iteration will detect the case of this point being outside the bracket interval.
B.2.11 Robust Variance Estimation
One problem with computing the sample variance using Equation (2.11) is that doing so requires storing all the samples . The storage requirements for this may be unacceptable—for example, for a Film implementation that is estimating per-pixel variance with thousands of samples per pixel. Equation (2.9) suggests another possibility: if we accumulate estimates of both and , then the sample variance could be estimated as
which only requires storing two values. This approach is numerically unstable, however, due to having a much larger magnitude than . Therefore, the following VarianceEstimator class, which computes an online estimate of variance without storing all the samples, uses Welford’s algorithm, which is numerically stable. Its implementation in pbrt is parameterized by a floating-point type so that, for example, double precision can be used even when pbrt is built to use single-precision Floats.
Welford’s algorithm computes two quantities: the sample mean and the sum of squares of differences between the samples and the sample mean, . In turn, gives the sample variance.
Both of these quantities can be computed incrementally. First, if is the sample mean of the first samples, then given an additional sample , the updated sample mean is
Next, if is the sum of squares of differences from the current mean,
then consider the difference , which is the quantity that when added to gives :
After some algebraic manipulation, this can be found to be equal to
which is comprised of quantities that are all readily available. The implementation of the VarianceEstimator Add() method is then just a matter of applying Equations (B.18) and (B.18).
Given these two quantities, VarianceEstimator can provide a number of useful statistical quantities.
It is also possible to merge two VarianceEstimators so that the result stores the same mean and variance estimates (modulo minor floating-point rounding error) as if a single VarianceEstimator had processed all the values seen by the two of them. This capability is particularly useful in parallel implementations, where separate threads may separately compute sample statistics that are merged later.
The Merge() method implements this operation, which we will not include here; see the “Further Reading” section for details of its derivation.
B.2.12 Square Matrices
The SquareMatrix class provides a representation of square matrices with dimensionality set at compile time via the template parameter N. It is an integral part of both the Transform class and pbrt’s color space conversion code.
The default constructor initializes the identity matrix. Other constructors (not included here) allow providing the values of the matrix directly or via a two-dimensional array of values. Alternatively, Zero() can be used to get a zero-valued matrix or Diag() can be called with N values to get the corresponding diagonal matrix.
All the basic arithmetic operations between matrices are provided, including multiplying them or dividing them by scalar values. Here is the implementation of the method that adds two matrices together.
The IsIdentity() checks whether the matrix is the identity matrix via a simple loop over its elements.
Indexing operators are provided as well. Because these methods return spans, the syntax for multidimensional indexing is the same as it is for regular C++ arrays: m[i][j].
The SquareMatrix class provides a matrix–vector multiplication function based on template classes to define the types of both the vector that is operated on and the result. It only requires that the result type has a default constructor and that both types allow element indexing via operator[]. Thus it can, for example, be used in pbrt’s color space conversion code to convert from RGB to XYZ via a call of the form Mul<XYZ>(m, rgb), where m is a SquareMatrix and rgb is of type RGB.
The Determinant() function returns the value of the matrix’s determinant using the standard formula. Specializations for and matrices are carefully written to use DifferenceOfProducts() for intermediate calculations of matrix minors in order to maximize accuracy in the result for those common cases.
Finally, there are both Transpose() and Inverse() functions. Like Determinant(), Inverse() has specializations for N up to 4 and then a general implementation for matrices of larger dimensionality.
The regular Inverse() function returns an unset optional value if the matrix has no inverse. If no recovery is possible in that case, InvertOrExit() can be used, allowing calling code to directly access the matrix result.
Given the SquareMatrix definition, it is easy to implement a LinearLeastSquares() function that finds a matrix that minimizes the least squares error of a mapping from one set of vectors to another. This function is used as part of pbrt’s infrastructure for modeling camera response curves.
B.2.13 Bézier Curves
Bézier curves, first introduced in Section 6.7 with the Curve shape, are polynomial functions that are widely used in graphics. They are specified by a number of control points that have the useful property that the curve passes through the first and last of them. Cubic Béziers, which are specified by four control points, are commonly used. pbrt’s functions for working with them are defined in the file util/splines.h.
They are commonly defined using polynomial basis functions called the Bernstein basis functions, though here we will focus on them through an approach called blossoming. The blossom of a cubic Bézier is defined by three stages of linear interpolation, starting with the original control points :
BlossomBezier() implements this computation, which we will see has a variety of uses. The type P of the control point is a template parameter, which makes it possible to call this function with any type for which a Lerp() function is defined.
The blossom gives the curve’s value at position . (To verify this for yourself, expand Equation (B.18) using , simplify, and compare to Equation (6.16).) Thus, implementation of the EvaluateCubicBezier() function is trivial. It too is a template function of the type of control point.
A second variant of EvaluateCubicBezier() also optionally returns the curve’s derivative at the evaluation point. This and the following Bézier functions could also be template functions based on the type of control point; for pbrt’s uses, however, only Point3f variants are required. We therefore implement them in terms of Point3f, if only to save the verbosity and slight obscurity of the templated variants.
With blossoming, the final two control points that are linearly interpolated to compute the curve value define a line that is tangent to the curve.
One edge case must be handled here: if, for example, the first three control points are coincident, then the derivative of the curve is legitimately 0 at . However, returning a zero-valued derivative in that case would be problematic since pbrt uses the derivative to compute the tangent vector of the curve. Therefore, this function returns the difference between the first and last control points in such cases.
SubdivideCubicBezier() splits a Bézier curve into two Bézier curves that together are equivalent to the original curve. The last control point of the first subdivided curve is the same as the first control point of the second one and the 7 total control points are specified by the blossoms , , , , , , and . There is no need to call BlossomCubicBezier() to evaluate them, however, as each one works out to be a simple combination of existing control points.
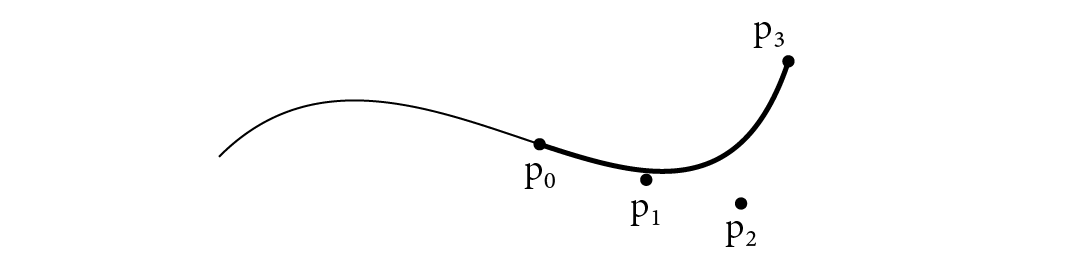
More generally, the four control points for the curve segment over the range to are given by the blossoms:
(see Figure B.5). CubicBezierControlPoints() implements this computation.
Bounding boxes of Curves can be efficiently computed by taking advantage of the convex hull property, a property of Bézier curves that says that they must lie within the convex hull of their control points. Therefore, the bounding box of the control points gives a conservative bound of the underlying curve. This bounding box is returned by the BoundCubicBezier() function.
A second variant of this function bounds a Bézier curve over a specified parametric range via a call to CubicBezierControlPoints().
B.2.14 Pseudo-Random Number Generation
pbrt uses an implementation of the PCG pseudo-random number generator (O’Neill 2014) to generate pseudo-random numbers. This generator not only passes a variety of rigorous statistical tests of randomness, but its implementation is also extremely efficient.
We wrap its implementation in a small random number generator class, RNG, which can be found in the files util/rng.h and util/rng.cpp. Random number generator implementation is an esoteric art; therefore, we will not include or discuss the implementation here but will describe the interfaces provided.
The RNG class provides three constructors. The first, which takes no arguments, sets the internal state to reasonable defaults. The others allow providing values that seed its state. The PCG random number generator actually allows the user to provide two 64-bit values to configure its operation: one chooses from one of different sequences of random numbers, while the second effectively selects a starting point within such a sequence. Many pseudo-random number generators only allow this second form of configuration, which alone is not as useful: having independent non-overlapping sequences of values rather than different starting points in a single sequence provides greater nonuniformity in the generated values.
RNGs should not be used in pbrt without either providing an initial sequence index via the constructor or a call to the SetSequence() method; otherwise, there is risk that different parts of the system will inadvertently use correlated sequences of pseudo-random values, which in turn could cause surprising errors.
The RNG class defines a template method Uniform() that returns a uniformly distributed random value of the specified type. A variety of specializations of this method are provided for basic arithmetic types.
The default implementation of Uniform() attempts to ensure that a useful error message is issued if it is invoked with an unsupported type.
A specialization for uint32_t uses the PCG algorithm to generate a 32-bit value. We will not include its implementation here, as it would be impenetrable without an extensive discussion of the details of the pseudo-random number generation approach it implements.
Given a source of pseudo-randomness, a variety of other specializations of Uniform() can be provided. For example, a uniform 64-bit unsigned integer can be generated by using the bits from two 32-bit random numbers.
Generating a uniformly distributed signed 32-bit integer requires surprisingly tricky code. The issue is that in C++, it is undefined behavior to assign a value to a signed integer that is larger than it can represent. Undefined behavior does not just mean that the result is undefined, but that, in principle, no further guarantees are made about correct program execution after it occurs. Therefore, the following code is carefully written to avoid integer overflow. In practice, a good compiler can be expected to optimize away the extra work.
A similar method returns pseudo-random int64_t values.
It is often useful to generate a value that is uniformly distributed in the range given a bound . The first two versions of pbrt effectively computed Uniform<int32_t>() % b to do so. That approach is subtly flawed—in the case that b does not evenly divide , there is higher probability of choosing any given value in the sub-range .
Therefore, the implementation here first computes the above remainder efficiently using 32-bit arithmetic and stores it in the variable threshold. Then, if the value returned by Uniform() is less than threshold, it is discarded and a new value is generated. The resulting distribution of values has a uniform distribution after the modulus operation, giving a uniformly distributed sample value.
The tricky declaration of the return value ensures that this variant of Uniform() is only available for integral types.
A specialization of Uniform() for floats generates a pseudo-random floating-point number in the half-open interval by multiplying a 32-bit random value by . Mathematically, this value is always less than one; it can be at most . However, some values still round to 1 when computed using floating-point arithmetic. That case is handled here by clamping to the largest representable float less than one. Doing so introduces a tiny bias, but not one that is meaningful for rendering applications.
An equivalent method for doubles is provided but is not included here.
With this random number generator, it is possible to step forward or back to a different spot in the sequence without generating all the intermediate values. The Advance() method provides this functionality.
B.2.15 Interval Arithmetic
Interval arithmetic is a technique that can be used to reason about the range of a function over some range of values and also to bound the round-off error introduced by a series of floating-point calculations. The Interval class provides functionality for both of these uses.
To understand the basic idea of interval arithmetic, consider, for example, the function . If we have an interval of values , then we can see that, over the interval, the range of is the interval . In other words, . More generally, all the basic operations of arithmetic have interval extensions that describe how they operate on intervals of values. For example, given two intervals and ,
In other words, if we add together two values where one is in the range and the second is in , then the result must be in the range . Interval arithmetic has the important property that the intervals that it gives are conservative. For example, if and if , then we know for sure that no value in causes to be negative.
When implemented in floating-point arithmetic, interval operations can be defined so that they result in intervals that bound the true value. Given a function that rounds a value that cannot exactly be represented as a floating-point value down to the next lower floating-point value and that similarly rounds up, interval addition can be defined as
Performing a series of floating-point calculations in this manner is the basis of running error analysis, which was described in Section 6.8.1.
pbrt uses interval arithmetic to compute error bounds for ray intersections with quadrics and also uses the interval-based Point3i class to store computed ray intersection points on surfaces. The zero-finding method used to find the extrema of moving bounding boxes in AnimatedTransform::BoundPointMotion() (included in the online edition) is also based on interval arithmetic.
The Interval class provides interval arithmetic capabilities using operator overloading to make it fairly easy to switch existing regular floating-point computations over to be interval-based.
Before we go further with Interval, we will define some supporting utility functions for performing basic arithmetic with specified rounding. Recall that the default with floating-point arithmetic is that results are rounded to the nearest representable floating-point value, with ties being rounded to the nearest even value (i.e., with a zero-valued low bit in its significand). However, in order to compute conservative intervals like those in Equation (B.18), it is necessary to specify different rounding modes for different operations, rounding down when computing the value at the lower range of the interval and rounding up at the upper range.
The IEEE floating-point standard requires capabilities to control the rounding mode, but unfortunately it is expensive to change it on modern CPUs. Doing so generally requires a flush of the execution pipeline, which may cost many tens of cycles. Therefore, pbrt provides utility functions that perform various arithmetic operations where the final value is then nudged up or down to the next representable float. This will lead to intervals that are slightly too large, sometimes nudging when it is not necessary, but for pbrt’s purposes it is preferable to paying the cost of changing the rounding mode.
Some GPUs provide intrinsic functions to perform these various operations directly, with the rounding mode specified as part of the instruction and with no performance cost. Alternative implementations of these functions, not included here, use those when they are available.
Beyond addition, there are equivalent methods that are not included here for subtraction, multiplication, division, the square root, and FMA.
An interval can be initialized with a single value or a pair of values that specify an interval with nonzero width.
It can also be specified by a value and an error bound. Note that the implementation uses rounded arithmetic functions to ensure a conservative interval.
A number of accessor methods provide information about the interval. An implementation of operator[], not included here, allows indexing the two bounding values.
An interval can be converted to a Float approximation to it, but only through an explicit cast, which ensures that intervals are not accidentally reduced to Floats in the middle of a computation, thus causing an inaccurate final interval.
InRange() method implementations check whether a given value is in the interval and whether two intervals overlap.
Negation of an interval is straightforward, as it does not require any rounding.
The addition operator just requires implementing Equation (B.18) with the appropriate rounding.
The subtraction operator and the += and -= operators follow the same pattern, so they are not included in the text.
Interval multiplication and division are slightly more involved: which of the low and high bounds of each of the two intervals is used to determine each of the bounds of the result depends on the signs of the values involved. Rather than incur the overhead of working out exactly which pairs to use, Interval’s implementation of the multiply operator computes all of them and then takes the minimum and maximum.
The division operator follows a similar form, though it must check to see if the divisor interval spans zero. If so, an infinite interval must be returned.
The interval Sqr() function is more than a shorthand; it is sometimes able to compute a tighter bound than would be found by multiplying an interval by itself using operator*. To see why, consider two independent intervals that both happen to have the range . Multiplying them together results in the interval . However, if we are multiplying an interval by itself, we know that there is no way that squaring it would result in a negative value. Therefore, if an interval with the bounds is multiplied by itself, it is possible to return the tighter interval instead.
A variety of additional arithmetic operations are provided by the Interval class, including Abs(), Min(), Max(), Sqrt(), Floor(), Ceil(), Quadratic(), and assorted trigonometric functions. See the pbrt source code for their implementations.
pbrt provides 3D vector and point classes that use Interval for the coordinate values. Here, the “fi” at the end of Vector3fi denotes “float interval.” These classes are easily defined thanks to the templated definition of the Vector3 and Point3 classes and the underlying Tuple3 class from Section 3.2.
In addition to the usual constructors, Vector3fi can be initialized by specifying a base vector and a second one that gives error bounds for each component.
Helper methods return error bounds for the vector components and indicate if the value stored has empty intervals.
The Point3fi class, not included here, similarly provides the capabilities of a Point3 using intervals for its coordinate values. It, too, provides Error() and IsExact() methods.