11.1 Volume Scattering Processes

There are three main physical processes that affect the distribution of radiance in an environment with participating media:

  • Absorption: the reduction in radiance due to the conversion of light to another form of energy, such as heat.
  • Emission: radiance that is added to the environment from luminous particles.
  • Scattering: radiance heading in one direction that is scattered to other directions due to collisions with particles.

The characteristics of all of these properties may be homogeneous or inhomogeneous. Homogeneous properties are constant throughout some region of space, while inhomogeneous properties vary throughout space. Figure 11.1 shows a simple example of volume scattering, where a spotlight shining through a homogeneous participating medium illuminates particles in the medium and casts a volumetric shadow.

Figure 11.1: Dragon Illuminated by a Spotlight through Fog. Light scattering from particles in the medium back toward the camera makes the spotlight’s illumination visible even in pixels where there are no visible surfaces that reflect it. The dragon blocks light, casting a volumetric shadow on the right side of the image. (Dragon model courtesy of the Stanford Computer Graphics Laboratory.)

All of these processes may have different behavior at different wavelengths of light. While wavelength-dependent emission can be handled in the same way that it is from surface emitters, wavelength-dependent absorption and scattering require special handling in Monte Carlo estimators. We will gloss past those details in this chapter, deferring discussion of them until Section 14.2.2.

Physically, these processes all happen discretely: a photon is absorbed by some particle or it is not. We will nevertheless model all of these as continuous processes, following the same assumptions as underlie our use of radiometry to model light in pbrt (Section 4.1). However, as we apply Monte Carlo to solve the integrals that describe this process, we will end up considering the effect of these processes at particular points in the scene, which we will term scattering events. Note that “scattering events” is a slight misnomer, since absorption is a possibility as well as scattering.

All the models in this chapter are based on the assumption that the positions of the particles are uncorrelated—in other words, that although their density may vary spatially, their positions are otherwise independent. (In the context of the colors of noise introduced in Section 8.1.6, the assumption is a white noise distribution of their positions.) This assumption does not hold for many types of physical media; for example, it is not possible for two particles to both be in the same point in space and so a true white noise distribution is not possible. See the “Further Reading” section at the end of the chapter for pointers to recent work in relaxing this assumption.

11.1.1 Absorption

Consider thick black smoke from a fire: the smoke obscures the objects behind it because its particles absorb light traveling from the object to the viewer. The thicker the smoke, the more light is absorbed. Figure 11.2 shows this effect with a realistic cloud model.

Figure 11.2: If a participating medium primarily absorbs light passing through it, it will have a dark appearance, as shown here. (a) A relatively dense medium leads to a more apparent boundary as well as a darker result. (b) A less dense medium gives a softer look, as more light makes it through the medium. (Cloud model courtesy of Walt Disney Animation Studios.)

Absorption is described by the medium’s absorption coefficient, sigma Subscript normal a , which is the probability density that light is absorbed per unit distance traveled in the medium. (Note that the medium absorption is distinct from the absorption coefficient used in specifying indices of refraction of conductors, as introduced in Section 9.3.6.) It is usually a spectrally varying quantity, though we will neglect the implications of that detail in this chapter and return to them in Section 14.2.2. Its units are reciprocal distance ( normal m Superscript negative 1 ), which means that sigma Subscript normal a can take on any nonnegative value; it is not required to be between 0 and 1, for instance. In general, the absorption coefficient may vary with both position normal p Subscript and direction omega Subscript , although the volume scattering code in pbrt models it as purely a function of position. We will therefore sometimes simplify notation by not including omega Subscript in the use of sigma Subscript normal a and other related scattering properties, though it is easy enough to reintroduce when it is relevant.

Figure 11.3 shows the effect of absorption along a very short segment of a ray. Some amount of radiance upper L Subscript normal i Baseline left-parenthesis normal p Subscript Baseline comma minus omega Subscript Baseline right-parenthesis is arriving at point normal p Subscript , and we would like to find the exitant radiance upper L Subscript normal o Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis after absorption in the differential volume. This change in radiance along the differential ray length normal d t is described by the differential equation

upper L Subscript normal o Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis minus upper L Subscript normal i Baseline left-parenthesis normal p Subscript Baseline comma minus omega Subscript Baseline right-parenthesis equals normal d upper L Subscript normal o Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals minus sigma Subscript normal a Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis upper L Subscript normal i Baseline left-parenthesis normal p Subscript Baseline comma minus omega Subscript Baseline right-parenthesis normal d t comma

which says that the differential reduction in radiance along the beam is a linear function of its initial radiance. (This is another instance of the linearity assumption in radiometry: the fraction of light absorbed does not vary based on the ray’s radiance, but is always a fixed fraction.)

Figure 11.3: Absorption reduces the amount of radiance along a ray through a participating medium. Consider a ray carrying incident radiance at a point normal p Subscript from direction minus omega Subscript . If the ray passes through a differential cylinder filled with absorbing particles, the change in radiance due to absorption by those particles is normal d upper L Subscript normal o Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals minus sigma Subscript normal a Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis upper L Subscript normal i Baseline left-parenthesis normal p Subscript Baseline comma minus omega Subscript Baseline right-parenthesis normal d t .

This differential equation can be solved to give the integral equation describing the total fraction of light absorbed for a ray. If we assume that the ray travels a distance d in direction omega Subscript through the medium starting at point normal p Subscript , the surviving portion of the original radiance is given by

normal e Superscript minus integral Subscript 0 Superscript d Baseline sigma Super Subscript normal a Superscript left-parenthesis normal p Super Subscript Superscript plus t omega Super Subscript Superscript comma omega Super Subscript Superscript right-parenthesis normal d t Baseline period

11.1.2 Emission

While absorption reduces the amount of radiance along a ray as it passes through a medium, emission increases it due to chemical, thermal, or nuclear processes that convert energy into visible light. Figure 11.4 shows emission in a differential volume, where we denote emitted radiance added to a ray per unit distance at a point normal p Subscript in direction omega Subscript by sigma Subscript normal a Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis upper L Subscript normal e Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis . Figure 11.5 shows the effect of emission with a data set from a physical simulation of an explosion.

Figure 11.4: The volume emission function upper L Subscript normal e Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis gives the change in radiance along a ray as it passes through a differential volume of emissive particles. The change in radiance due to emission per differential distance is given by Equation (11.1).

Figure 11.5: A Participating Medium Where the Dominant Volumetric Effect Is Emission. (Scene courtesy of Jim Price.)

The differential equation that gives the change in radiance due to emission is

normal d upper L Subscript normal o Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals sigma Subscript normal a Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis upper L Subscript normal e Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis normal d t period
(11.1)

The presence of sigma Subscript normal a on the right hand side stems from the connection between how efficiently an object absorbs light and how efficiently it emits it, as was introduced in Section 4.4.1. That factor also ensures that the corresponding term has units of radiance when the differential equation is converted to an integral equation.

Note that this equation incorporates the assumption that the emitted light upper L Subscript normal e is not dependent on the incoming light upper L Subscript normal i . This is always true under the linear optics assumptions that pbrt is based on.

11.1.3 Out Scattering and Attenuation

The third basic light interaction in participating media is scattering. As a ray passes through a medium, it may collide with particles and be scattered in different directions. This has two effects on the total radiance that the beam carries. It reduces the radiance exiting a differential region of the beam because some of it is deflected to different directions. This effect is called out scattering (Figure 11.6) and is the topic of this section. However, radiance from other rays may be scattered into the path of the current ray; this in-scattering process is the subject of the next section. We will sometimes say that these two forms of scattering are real scattering, to distinguish them from null scattering, which will be introduced in Section 11.2.1.

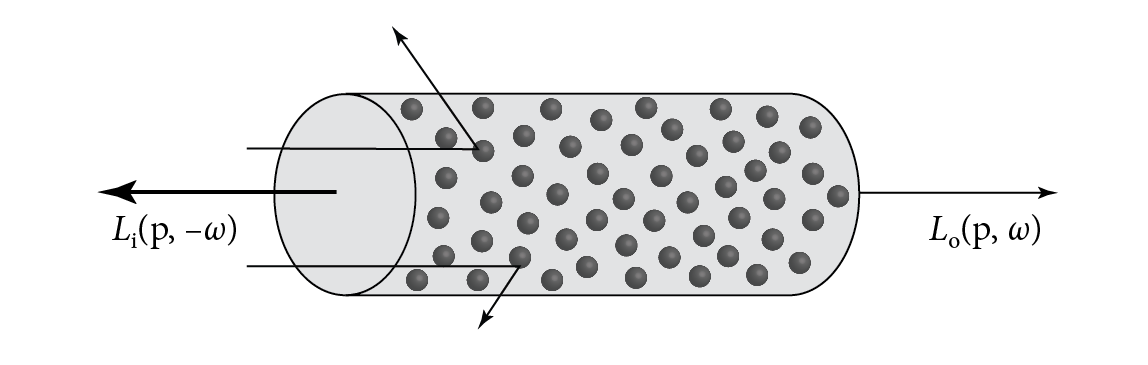
Figure 11.6: Like absorption, out scattering also reduces the radiance along a ray. Light that hits particles may be scattered in another direction such that the radiance exiting the region in the original direction is reduced.

The probability of an out-scattering event occurring per unit distance is given by the scattering coefficient, sigma Subscript normal s . Similar to absorption, the reduction in radiance along a differential length normal d t due to out scattering is given by

normal d upper L Subscript normal o Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals minus sigma Subscript normal s Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis upper L Subscript normal i Baseline left-parenthesis normal p Subscript Baseline comma minus omega Subscript Baseline right-parenthesis normal d t period

The total reduction in radiance due to absorption and out scattering is given by the sum sigma Subscript normal a Baseline plus sigma Subscript normal s . This combined effect of absorption and out scattering is called attenuation or extinction. The sum of these two coefficients is denoted by the attenuation coefficient  sigma Subscript normal t :

sigma Subscript normal t Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals sigma Subscript normal a Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis plus sigma Subscript normal s Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis period

Two values related to the attenuation coefficient will be useful in the following. The first is the single-scattering albedo, which is defined as

rho left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals StartFraction sigma Subscript normal s Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis Over sigma Subscript normal t Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis EndFraction period

Under the assumptions of radiometry, the single-scattering albedo is always between 0 and 1. It describes the probability of scattering (versus absorption) at a scattering event. The second is the mean free path, 1 slash sigma Subscript normal t Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis , which gives the average distance that a ray travels in a medium with attenuation coefficient sigma Subscript normal t Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis before interacting with a particle.

11.1.4 In Scattering

While out scattering reduces radiance along a ray due to scattering in different directions, in scattering accounts for increased radiance due to scattering from other directions (Figure 11.7). Figure 11.8 shows the effect of in scattering with the cloud model. There is no absorption there, corresponding to a single scattering albedo of 1. Light thus scatters many times inside the cloud, giving it a very different appearance.

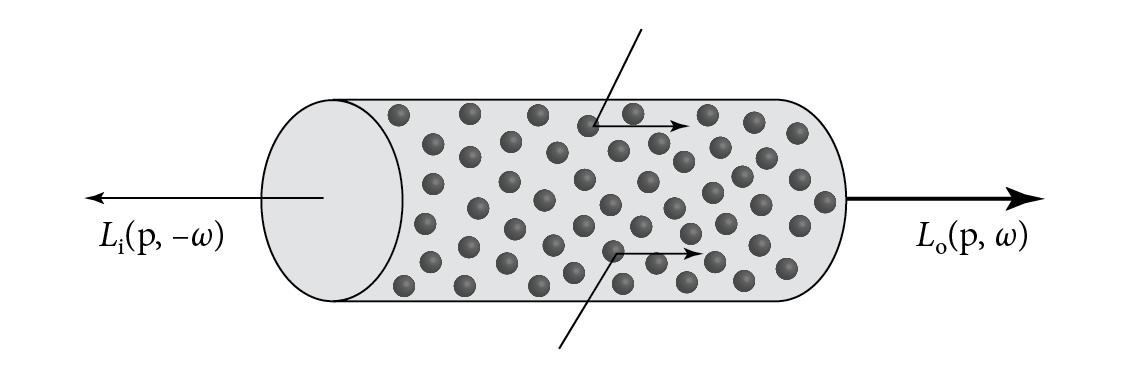
Figure 11.7: In scattering accounts for the increase in radiance along a ray due to scattering of light from other directions. Radiance from outside the differential volume is scattered along the direction of the ray and added to the incoming radiance.

Figure 11.8: In Scattering with the Cloud Model. For these scenes, there is no absorption and only scattering, which gives a substantially different result than the clouds in Figure 11.2. (a) Relatively dense cloud. (b) Thinner cloud. (Cloud model courtesy of Walt Disney Animation Studios.)

Assuming that the separation between particles is at least a few times the lengths of their radii, it is possible to ignore inter-particle interactions when describing scattering at a particular location. Under this assumption, the phase function p left-parenthesis omega Subscript Baseline comma omega prime Subscript Baseline right-parenthesis describes the angular distribution of scattered radiation at a point; it is the volumetric analog to the BSDF. The BSDF analogy is not exact, however. For example, phase functions have a normalization constraint: for all omega Subscript , the condition

integral Underscript script upper S squared Endscripts p left-parenthesis omega Subscript Baseline comma omega prime Subscript Baseline right-parenthesis normal d omega Subscript Baseline Superscript prime Baseline equals 1
(11.2)

must hold. This constraint means that phase functions are probability distributions for scattering in a particular direction.

The total added radiance per unit distance is given by the source function  upper L Subscript normal s Superscript :

normal d upper L Subscript normal o Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals sigma Subscript normal t Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis upper L Subscript normal s Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis normal d t period

It accounts for both volume emission and in scattering:

upper L Subscript normal s Superscript Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis equals StartFraction sigma Subscript normal a Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis Over sigma Subscript normal t Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis EndFraction upper L Subscript normal e Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis plus StartFraction sigma Subscript normal s Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis Over sigma Subscript normal t Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript Baseline right-parenthesis EndFraction integral Underscript script upper S squared Endscripts p left-parenthesis normal p Subscript Baseline comma omega Subscript normal i Baseline comma omega Subscript Baseline right-parenthesis upper L Subscript normal i Baseline left-parenthesis normal p Subscript Baseline comma omega Subscript normal i Baseline right-parenthesis normal d omega Subscript normal i Baseline period
(11.3)

The in-scattering portion of the source function is the product of the albedo and the amount of added radiance at a point, which is given by the spherical integral of the product of incident radiance and the phase function. Note that the source function is very similar to the scattering equation, Equation (4.14); the main difference is that there is no cosine term since the phase function operates on radiance rather than differential irradiance.