11.2 Transmittance
The scattering processes in Section 11.1 are all specified in terms of their local effect at points in space. However, in rendering, we are usually interested in their aggregate effects on radiance along a ray, which usually requires transforming the differential equations to integral equations that can be solved using Monte Carlo. The reduction in radiance between two points on a ray due to extinction is a quantity that will often be useful; for example, we will need to estimate this value to compute the attenuated radiance from a light source that is incident at a point on a surface in scenes with participating media.
Given the attenuation coefficient , the differential equation that describes extinction,
can be solved to find the beam transmittance , which gives the fraction of radiance that is transmitted between two points:
where is the distance between and , and is the normalized direction vector between them. Note that the transmittance is always between 0 and 1. Thus, if exitant radiance from a point on a surface in a given direction is given by , then after accounting for extinction the incident radiance at another point in direction is
This idea is illustrated in Figure 11.9.
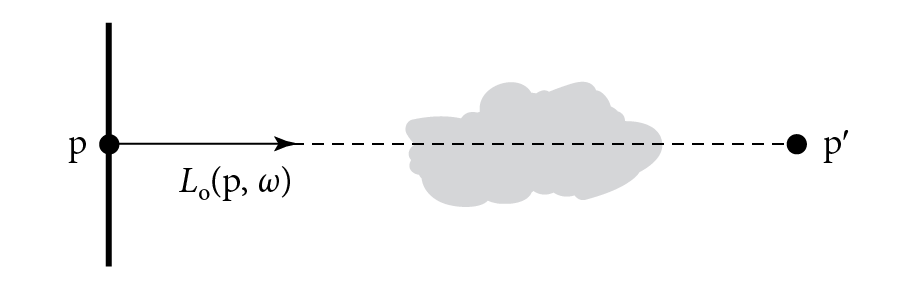
Not only is transmittance useful for modeling the attenuation of light within participating media, but accounting for transmittance along shadow rays makes it possible to accurately model shadowing on surfaces due to the effect of media; see Figure 11.10.

Two useful properties of beam transmittance are that transmittance from a point to itself is 1, , and in a vacuum and so for all . Furthermore, if the attenuation coefficient satisfies the directional symmetry or does not vary with direction and only varies as a function of position, then the transmittance between two points is the same in both directions:
This property follows directly from Equation (11.5).
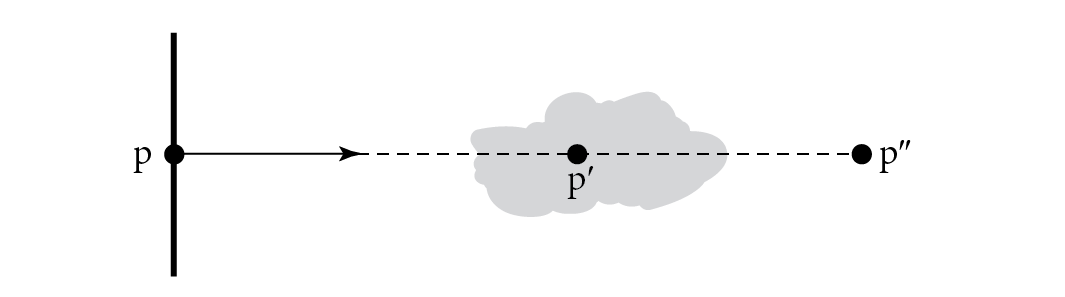
Another important property, true in all media, is that transmittance is multiplicative along points on a ray:
for all points between and (Figure 11.11). This property is useful for volume scattering implementations, since it makes it possible to incrementally compute transmittance at multiple points along a ray: transmittance from the origin to a point can be computed by taking the product of transmittance to a previous point and the transmittance of the segment between the previous and the current point .
The negated exponent in the definition of in Equation (11.5) is called the optical thickness between the two points. It is denoted by the symbol :
In a homogeneous medium, is a constant, so the integral that defines is trivially evaluated, giving Beer’s law:
It may appear that a straightforward application of Monte Carlo could be used to compute the beam transmittance in inhomogeneous media. Equation (11.5) consists of a 1D integral over a ray’s parametric position that is then exponentiated; given a method to sample distances along the ray according to some distribution , one could evaluate the estimator:
However, even if the estimator in square brackets is an unbiased estimator of the optical thickness along the ray, the estimate of transmittance is not unbiased and will actually underestimate its value: . (This state of affairs is explained by Jensen’s inequality and the fact that is a convex function.)
The error introduced by estimators of the form of Equation (11.8) decreases as error in the estimate of the beam transmittance decreases. For many applications, this error may be acceptable—it is still widespread practice in graphics to estimate in some manner, e.g., via a Riemann sum, and then to compute the transmittance that way. However, it is possible to derive an alternative equation for transmittance that allows unbiased estimation; that is the approach used in pbrt.
First, we will consider the change in radiance between two points and along the ray. Integrating Equation (11.4) and dropping the directional dependence of for notational simplicity, we can find that
where, as before, is the distance between and and is the normalized vector from to .
The transmittance is the fraction of the original radiance, and so . Thus, if we divide Equation (11.9) by and rearrange terms, we can find that
We have found ourselves with transmittance defined recursively in terms of an integral that includes transmittance in the integrand; although this may seem to be making the problem more complex than it was before, this definition makes it possible to apply Monte Carlo to the integral and to compute unbiased estimates of transmittance. However, it is difficult to sample this integrand well; in practice, estimates of it will have high variance. Therefore, the following section will introduce an alternative formulation of it that is amenable to sampling and makes a number of efficient solution techniques possible.
11.2.1 Null Scattering
The key idea that makes it possible to derive a more easily sampled transmittance integral is an approach known as null scattering. Null scattering is a mathematical formalism that can be interpreted as introducing an additional type of scattering that does not correspond to any type of physical scattering process but is specified so that it has no effect on the distribution of light. In doing so, null scattering makes it possible to treat inhomogeneous media as if they were homogeneous, which makes it easier to apply sampling algorithms to inhomogeneous media. (In Chapter 14, we will see that it is a key foundation for volumetric light transport algorithms beyond transmittance estimation.)
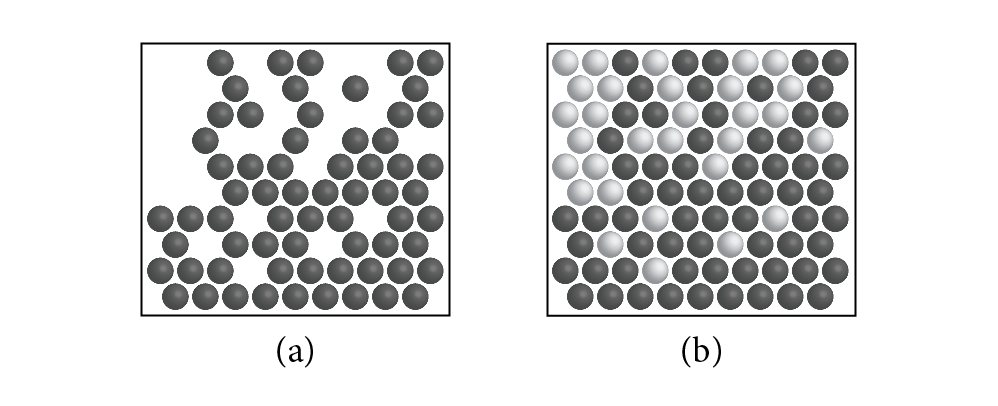
We will start by defining the null-scattering coefficient . Similar to the other scattering coefficients, it gives the probability of a null-scattering event per unit distance traveled in the medium. Here, we will define via a constant majorant that is greater than or equal to at all points in the medium:
Thus, the total scattering coefficient is uniform throughout the medium. (This idea is illustrated in Figure 11.12.)
With this definition of , we can rewrite Equation (11.4) in terms of the majorant and the null-scattering coefficient:
We will not include the full derivation here, but just as with Equation (11.10), this equation can be integrated over the segment of a ray and divided by the initial radiance to find an equation for the transmittance. The result is:
Note that with this expression of transmittance and a homogeneous medium, and the integral disappears. The first term then corresponds to Beer’s law. For inhomogeneous media, the first term can be seen as computing an underestimate of the true transmittance, where the integral then accounts for the rest of it.
To compute Monte Carlo estimates of Equation (11.13), we would like to sample a distance from some distribution that is proportional to the integrand and then apply the regular Monte Carlo estimator. A convenient sampling distribution is the probability density function (PDF) of the exponential distribution that is derived in Section A.4.2. In this case, the PDF associated with is
and a corresponding sampling recipe is available via the SampleExponential() function.
Because is nonzero over the range , the sampling algorithm will sometimes generate samples , which may seem to be undesirable. However, although we could define a PDF for the exponential function limited to , sampling from leads to a simple way to terminate the recursive evaluation of transmittance. To see why, consider rewriting the second term of Equation (11.13) as the sum of two integrals that cover the range :
If the Monte Carlo estimator is applied to this sum, we can see that the value of with respect to determines which integrand is evaluated and thus that sampling can be conveniently interpreted as a condition for ending the recursive estimation of Equation (11.13).
Given the decision to sample from , perhaps the most obvious approach for estimating the value of Equation (11.13) is to sample in this way and to directly apply the Monte Carlo estimator, which gives
This estimator is known as the next-flight estimator. It has the advantage that it has zero variance for homogeneous media, although interestingly it is often not as efficient as other estimators for inhomogeneous media.
Other estimators randomly choose between the two terms of Equation (11.13) and only evaluate one of them. If we define as the discrete probability of evaluating the first term, transmittance can be estimated by
The ratio tracking estimator is the result from setting . Then, the first case of Equation (11.16) yields a value of 1. We can further combine the choice between the two cases with sampling using the fact that the probability that is equal to . (This can be seen using ’s cumulative distribution function (CDF), Equation (A.17).) After simplifying, the resulting estimator works out to be:
If the recursive evaluations are expanded out, ratio tracking leads to an estimator of the form
where are the series of values that are sampled from and where successive values are sampled starting from the previous one until one is sampled past the endpoint. Ratio tracking is the technique that is implemented to compute transmittance in pbrt’s light transport routines in Chapter 14.
A disadvantage of ratio tracking is that it continues to sample the medium even after the transmittance has become very small. Russian roulette can be used to terminate recursive evaluation to avoid this problem. If the Russian roulette termination probability at each sampled point is set to be equal to the ratio of and , then the scaling cancels and the estimator becomes
Thus, recursive estimation of transmittance continues either until termination due to Russian roulette or until the sampled point is past the endpoint. This approach is the track-length transmittance estimator, also known as delta tracking.
A physical interpretation of delta tracking is that it randomly decides whether the ray interacts with a true particle or a fictitious particle at each scattering event. Interactions with fictitious particles (corresponding to null scattering) are ignored and the algorithm continues, restarting from the sampled point. Interactions with true particles cause extinction, in which case 0 is returned. If a ray makes it through the medium without extinction, the value 1 is returned.
Delta tracking can also be used to sample positions along a ray with probability proportional to . The algorithm is given by the following pseudocode, which assumes that the function u() generates a uniform random number between 0 and 1 and where the recursion has been transformed into a loop: