14.1 The Equation of Transfer
The equation of transfer is the fundamental equation that governs the behavior of light in a medium that absorbs, emits, and scatters radiation. It accounts for all the volume scattering processes described in Chapter 11—absorption, emission, in scattering, and out scattering—to give an equation that describes the equilibrium distribution of radiance. The light transport equation is in fact a special case of it, simplified by the lack of participating media and specialized for scattering from surfaces. (We will equivalently refer to the equation of transfer as the volumetric light transport equation.)
In its most basic form, the equation of transfer is an integro-differential equation that describes how the radiance along a beam changes at a point in space. It can be derived by subtracting the effects of the scattering processes that reduce energy along a beam (absorption and out scattering) from the processes that increase energy along it (emission and in scattering).
To start, recall the source function from Section 11.1.4: it gives the change in radiance at a point in a direction due to emission and in-scattered light from other points in the medium:
The source function accounts for all the processes that add radiance to a ray.
The attenuation coefficient, , accounts for all processes that reduce radiance at a point: absorption and out scattering. The differential equation that describes its effect, Equation (11.4), is
The overall differential change in radiance at a point along a ray is found by adding these two effects together to get the integro-differential form of the equation of transfer:
(The modulation of the source function accounts for the medium’s density at the point.)
With suitable boundary conditions, this equation can be transformed to a pure integral equation that describes the effect of participating media from the infinite number of points along a ray. For example, if we assume that there are no surfaces in the scene so that the rays are never blocked and have an infinite length, the integral equation of transfer is
(See Figure 14.1.) The meaning of this equation is reasonably intuitive: it just says that the radiance arriving at a point from a given direction is determined by accumulating the radiance added at all points along the ray. The amount of added radiance at each point along the ray that reaches the ray’s origin is reduced by the beam transmittance to the point.

More generally, if there are reflecting or emitting surfaces in the scene, rays do not necessarily have infinite length and the first surface that a ray hits affects its radiance, adding outgoing radiance from the surface at the point and preventing radiance from points along the ray beyond the intersection point from contributing to radiance at the ray’s origin. If a ray (, ) intersects a surface at some point at a parametric distance along the ray, then the integral equation of transfer is
where are points along the ray (Figure 14.2).
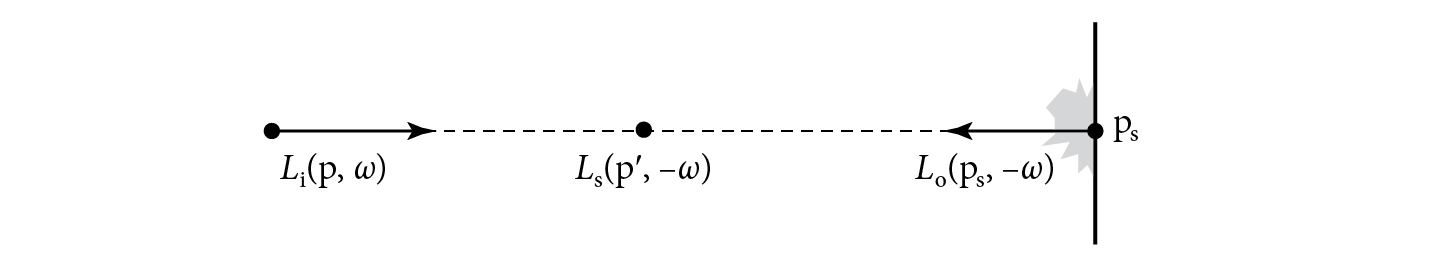
This equation describes the two effects that contribute to radiance along the ray. First, reflected radiance back along the ray from the surface is given by the term, which gives the emitted and reflected radiance from the surface. This radiance may be attenuated by the participating media; the beam transmittance from the ray origin to the point accounts for this. The second term accounts for the added radiance along the ray due to volumetric scattering and emission up to the point where the ray intersects the surface; points beyond that one do not affect the radiance along the ray.
14.1.1 Null-Scattering Extension
In Section 11.2.1 we saw the value of null scattering, which made it possible to sample from a modified transmittance equation and to compute unbiased estimates of the transmittance between two points using algorithms like delta tracking and ratio tracking. Null scattering can be applied in a similar way to the equation of transfer, giving similar benefits.
In order to simplify notation in the following, we will assume that the various scattering coefficients do not vary as a function of direction. As before, we will also assume that the null-scattering coefficient is nonnegative and has been set to homogenize the medium’s density to a fixed majorant . Neither of these simplifications affect the course of the following derivations; both generalizations could be easily reintroduced.
A null-scattering generalization of the equation of transfer can be found using the relationship from Equation (11.11). If that substitution is made in the integro-differential equation of transfer, Equation (14.1), and the boundary condition of a surface at distance along the ray is applied, then the result can be transformed into the pure integral equation
where , as before, and we have introduced to denote the majorant transmittance that accounts for both regular attenuation and null scattering. Using the same convention as before that is the distance between points and , it is
The null-scattering source function is the source function from Equation (11.3) plus a new third term:
Because it includes attenuation due to null scattering, is always less than or equal to the actual transmittance. Thus, the product in Equation (14.3) may be less than the actual contribution of radiance leaving the surface, . However, any such deficiency is made up for by the last term of Equation (14.5).
14.1.2 Evaluating the Equation of Transfer
The factor in the null-scattering equation of transfer gives a convenient distribution for sampling distances along the ray in the medium that leads to the volumetric path-tracing algorithm, which we will now describe. (The algorithm we will arrive at is sometimes described as using delta tracking to solve the equation of transfer, since that is the sampling technique it uses for finding the locations of absorption and scattering events.)
If we assume for now that there is no geometry in the scene, then the null-scattering equation of transfer, Equation (14.3), simplifies to
Thanks to null scattering having made the majorant medium homogeneous, can be sampled exactly. The first step in the path-tracing algorithm is to sample a point from its distribution, giving the estimator
From Section A.4.2, we know that the probability density function (PDF) for sampling a distance from the exponential distribution is , and so the estimator simplifies to
What is left is to evaluate .
Because , the initial factors in each term of Equation (14.5) can be considered to be three probabilities that sum to 1. If one of the three terms is randomly selected according to its probability and the rest of the term is evaluated without that factor, the expected value of the result is equal to . Considering how to evaluate each of the terms:
- If the term is chosen, then the emission at is returned and sampling terminates.
- For the term, the integral over the sphere of directions must be estimated. A direction is sampled from some distribution and recursive evaluation of then proceeds, weighted by the ratio of the phase function and the probability of sampling the direction .
- If the null-scattering term is selected, is to be evaluated, which can be handled recursively as well.
For the full equation of transfer that includes scattering from surfaces, both the surface-scattering term and the integral over the ray’s extent lead to recursive evaluation of the equation of transfer. In the context of path tracing, however, we would like to only evaluate one of the terms in order to avoid an exponential increase in work. We will therefore start by defining a probability of estimating the surface-scattering term; volumetric scattering is evaluated otherwise. Given such a , the Monte Carlo estimator
gives in expectation.
A good choice for is that it be equal to . Surface scattering is then evaluated with a probability proportional to the transmittance to the surface and the ratio is equal to 1, leaving just the factor. Furthermore, a sampling trick can be used to choose between the two terms: if a sample is taken from ’s distribution, then the probability that is equal to . (This can be shown by integrating ’s PDF to find its cumulative distribution function (CDF) and then considering the value of its CDF at .) Using this technique and then making the same simplifications that brought us to Equation (14.6), we arrive at the estimator
From this point, outgoing radiance from a surface can be estimated using techniques that were introduced in Chapter 13, and can be estimated as described earlier.
14.1.3 Sampling the Majorant Transmittance
We have so far presented volumetric path tracing with the assumption that is constant along the ray and thus that is a single exponential function. However, those assumptions are not compatible with the segments of piecewise-constant majorants that Medium implementations provide with their RayMajorantIterators. We will now resolve this incompatibility.
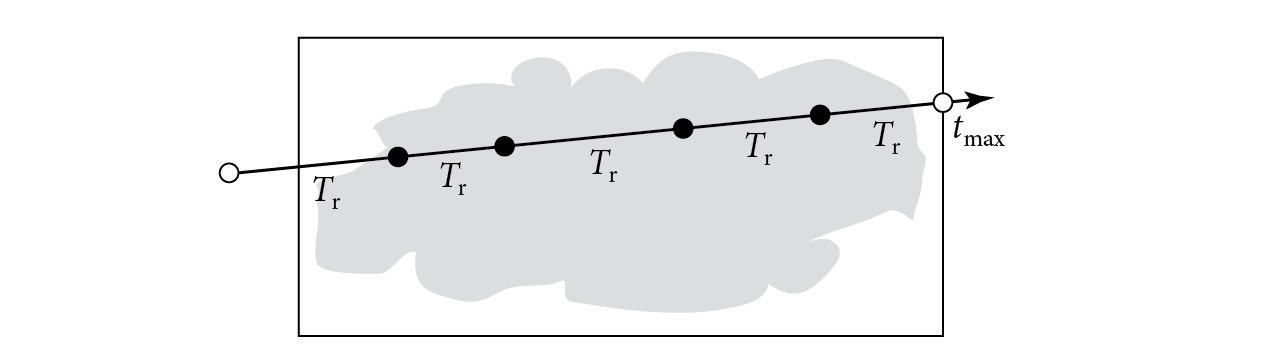
Figure 14.3 shows example majorants along a ray, the optical thickness that they integrate to, and the resulting majorant transmittance function. The transmittance function is continuous and strictly decreasing, though at a rate that depends on the majorant at each point along the ray. If integration starts from , and we denote the th segment’s majorant as and its endpoint as , the transmittance can be written as
where is the transmittance function for the th segment and the point is the endpoint of the th segment. (This relationship uses the multiplicative property of transmittance from Equation (11.6).)
Given the general task of estimating an integral of the form
with and , it is useful to rewrite the integral to be over the individual majorant segments, which gives
Note that each term’s contribution is modulated by the transmittances and majorants from the previous segments.
The form of Equation (14.8) hints at a sampling strategy: we start by sampling a value from ’s distribution ; if is less than , then we evaluate the estimator at the sampled point :
Applying the same ideas that led to Equation (14.7), we otherwise continue and consider the second term, drawing a sample from ’s distribution, starting at . If the sampled point is before the segment’s endpoint, , then we have the estimator
Because the probability that is equal to , the estimator for the second term again simplifies to . Otherwise, following this sampling strategy for subsequent segments similarly leads to the same simplified estimator in the end. It can furthermore be shown that the probability that no sample is generated in any of the segments is equal to the full majorant transmittance from 0 to , which is exactly the probability required for the surface/volume estimator of Equation (14.7).
The SampleT_maj() function implements this sampling strategy, handling the details of iterating over RayMajorantSegments and sampling them. Its functionality will be used repeatedly in the following volumetric integrators.
In addition to a ray and an endpoint along it specified by tMax, SampleT_maj() takes a single uniform sample and an RNG to use for generating any necessary additional samples. This allows it to use a well-distributed value from a Sampler for the first sampling decision along the ray while it avoids consuming a variable and unbounded number of sample dimensions if more are needed (recall the discussion of the importance of consistency in sample dimension consumption in Section 8.3).
The provided SampledWavelengths play their usual role, though the first of them has additional meaning: for media with scattering properties that vary with wavelength, the majorant at the first wavelength is used for sampling. The alternative would be to sample each wavelength independently, though that would cause an explosion in samples to be evaluated in the context of algorithms like path tracing. Sampling a single wavelength can work well for evaluating all wavelengths’ contributions if multiple importance sampling (MIS) is used; this topic is discussed further in Section 14.2.2.
A callback function is the last parameter passed to SampleT_maj(). This is a significant difference from pbrt’s other sampling methods, which all generate a single sample (or sometimes, no sample) each time they are called. When sampling media that has null scattering, however, often a succession of samples are needed along the same ray. (Delta tracking, described in Section 11.2.1, is an example of such an algorithm.) The provided callback function is therefore invoked by SampleT_maj() each time a sample is taken. After the callback processes the sample, it should return a Boolean value that indicates whether sampling should recommence starting from the provided sample. With this implementation approach, SampleT_maj() can maintain state like the RayMajorantIterator between samples along a ray, which improves efficiency.
The signature of the callback function should be the following:
Each invocation of the callback is passed a sampled point along the ray, the associated MediumProperties and for the medium at that point, and the majorant transmittance . The first time callback is invoked, the majorant transmittance will be from the ray origin to the sample; any subsequent invocations give the transmittance from the previous sample to the current one.
After sampling concludes, SampleT_maj() returns the majorant transmittance from the last sampled point in the medium (or the ray origin, if no samples were generated) to the ray’s endpoint (see Figure 14.4).
As if all of this was not sufficiently complex, the implementation of SampleT_maj() starts out with some tricky C++ code. There is a second variant of SampleT_maj() we will introduce shortly that is templated based on the concrete type of Medium being sampled. In order to call the appropriate template specialization, we must determine which type of Medium the ray is passing through. Conceptually, we would like to do something like the following, using the TaggedPointer::Is() method:
However, enumerating all the media that are implemented in pbrt in the SampleT_maj() function is undesirable: that would add an unexpected and puzzling additional step for users who wanted to extend the system with a new Medium. Therefore, the first SampleT_maj() function uses the dynamic dispatch capability of the Medium’s TaggedPointer along with a generic lambda function, sample, to determine the Medium’s type. TaggedPointer::Dispatch() ends up passing the Medium pointer back to sample; because the parameter is declared as auto, it then takes on the actual type of the medium when it is invoked. Thus, the following function has equivalent functionality to the code above but naturally handles all the media that are listed in the Medium class declaration without further modification.
With the concrete type of the medium available, we can proceed with the second instance of SampleTmaj(), which can now be specialized based on that type.
The function starts by normalizing the ray’s direction so that parametric distance along the ray directly corresponds to distance from the ray’s origin. This simplifies subsequent transmittance computations in the remainder of the function. Since normalization scales the direction’s length, the tMax endpoint must also be updated so that it corresponds to the same point along the ray.
Since the actual type of the medium is known and because all Medium implementations must define a MajorantIterator type (recall Section 11.4.1), the medium’s iterator type can be directly declared as a stack-allocated variable. This gives a number of benefits: not only is the expense of dynamic allocation avoided, but subsequent calls to the iterator’s Next() method in this function are regular method calls that can even be expanded inline by the compiler; no dynamic dispatch is necessary for them. An additional benefit of knowing the medium’s type is that the appropriate SampleRay() method can be called directly without incurring the cost of dynamic dispatch here.
With an iterator initialized, sampling along the ray can proceed. The T_maj variable declared here tracks the accumulated majorant transmittance from the ray origin or the previous sample along the ray (depending on whether a sample has yet been generated).
If the iterator has no further majorant segments to provide, then sampling is complete. In this case, it is important to return any majorant transmittance that has accumulated in T_maj; that represents the remaining transmittance to the ray’s endpoint. Otherwise, a few details are attended to before sampling proceeds along the segment.
If the majorant has the value 0 in the first wavelength, then there is nothing to sample along the segment. It is important to handle this case, since otherwise the subsequent call to SampleExponential() in this function would return an infinite value that would subsequently lead to not-a-number values. Because the other wavelengths may not themselves have zero-valued majorants, we must still update T_maj for the segment’s majorant transmittance even though the transmittance for the first wavelength is unchanged.
One edge case must be attended to before the exponential function is called. If tMax holds the IEEE floating-point infinity value, then dt will as well; it then must be bumped down to the largest finite Float. This is necessary because with floating-point arithmetic, zero times infinity gives a not-a-number value (whereas any nonzero value times infinity gives infinity). Otherwise, for any wavelengths with zero-valued sigma_maj, not-a-number values would be passed to FastExp().
The implementation otherwise tries to generate a sample along the current segment. This work is inside a while loop so that multiple samples may be generated along the segment.
In the usual case, a distance is sampled according to the PDF . Separate cases handle a sample that is within the current majorant segment and one that is past it.
One detail to note in this fragment is that as soon as the uniform sample u has been used, a replacement is immediately generated using the provided RNG. In this way, the method maintains the invariant that u is always a valid independent sample value. While this can lead to a single excess call to RNG::Uniform() each time SampleT_maj() is called, it ensures the initial u value provided to the method is used only once.
For a sample within the segment’s extent, the final majorant transmittance to be passed to the callback is found by accumulating the transmittance from tMin to the sample point. The rest of the necessary medium properties can be found using SamplePoint(). If the callback function returns false to indicate that sampling should conclude, then we have a doubly nested while loop to break out of; a break statement takes care of the inner one, and setting done to true causes the outer one to terminate.
If true is returned by the callback, indicating that sampling should restart at the sample that was just generated, then the accumulated transmittance is reset to 1 and tMin is updated to be at the just-taken sample’s position.
If the sampled distance is past the end of the segment, then there is no medium interaction along it and it is on to the next segment, if any. In this case, majorant transmittance up to the end of the segment must be accumulated into T_maj so that the complete majorant transmittance along the ray is provided with the next valid sample (if any).
14.1.4 Generalized Path Space
Just as it was helpful to express the light transport equation (LTE) as a sum over paths of scattering events, it is also helpful to express the null-scattering integral equation of transfer in this form. Doing so makes it possible to apply variance reduction techniques like multiple importance sampling and is a prerequisite for constructing participating medium-aware bidirectional integrators.
Recall how, in Section 13.1.4, the surface form of the LTE was repeatedly substituted into itself to derive the path space contribution function for a path of length
where the throughput was defined as
This previous definition only works for surfaces, but using a similar approach of substituting the integral equation of transfer, a medium-aware path integral can be derived. The derivation is laborious and we will just present the final result here. (The “Further Reading” section has a pointer to the full derivation.)
Previously, integration occurred over a Cartesian product of surface locations . Now, we will need a formal way of writing down an integral over an arbitrary sequence of each of 2D surface locations , 3D positions in a participating medium where actual scattering occurs, and 3D positions in a participating medium where null scattering occurs. (The two media and represent the same volume of space with the same scattering properties, but we will find it handy to distinguish between them in the following.)
First, we will focus only on a specific arrangement of surface and medium vertices encoded in a configuration vector . The associated set of paths is given by a Cartesian product of surface locations and medium locations,
The set of all paths of length is the union of the above sets over all possible configuration vectors:
Next, we define a measure, which provides an abstract notion of the volume of a subset that is essential for integration. The measure we will use simply sums up the product of surface area and volume associated with the individual vertices in each of the path spaces of specific configurations.
The measure for null-scattering vertices incorporates a Dirac delta distribution to limit integration to be along the line between successive real-scattering vertices.
The generalized path contribution can now be written as
where
Due to the measure defined earlier, the generalized path contribution is a sum of many integrals considering all possible sequences of surface, volume, and null-scattering events.
The full set of path vertices include both null- and real-scattering events. We will find it useful to use to denote the subset of them that represent real scattering (see Figure 14.5). Note a given real-scattering vertex will generally have a different index value in the full path.
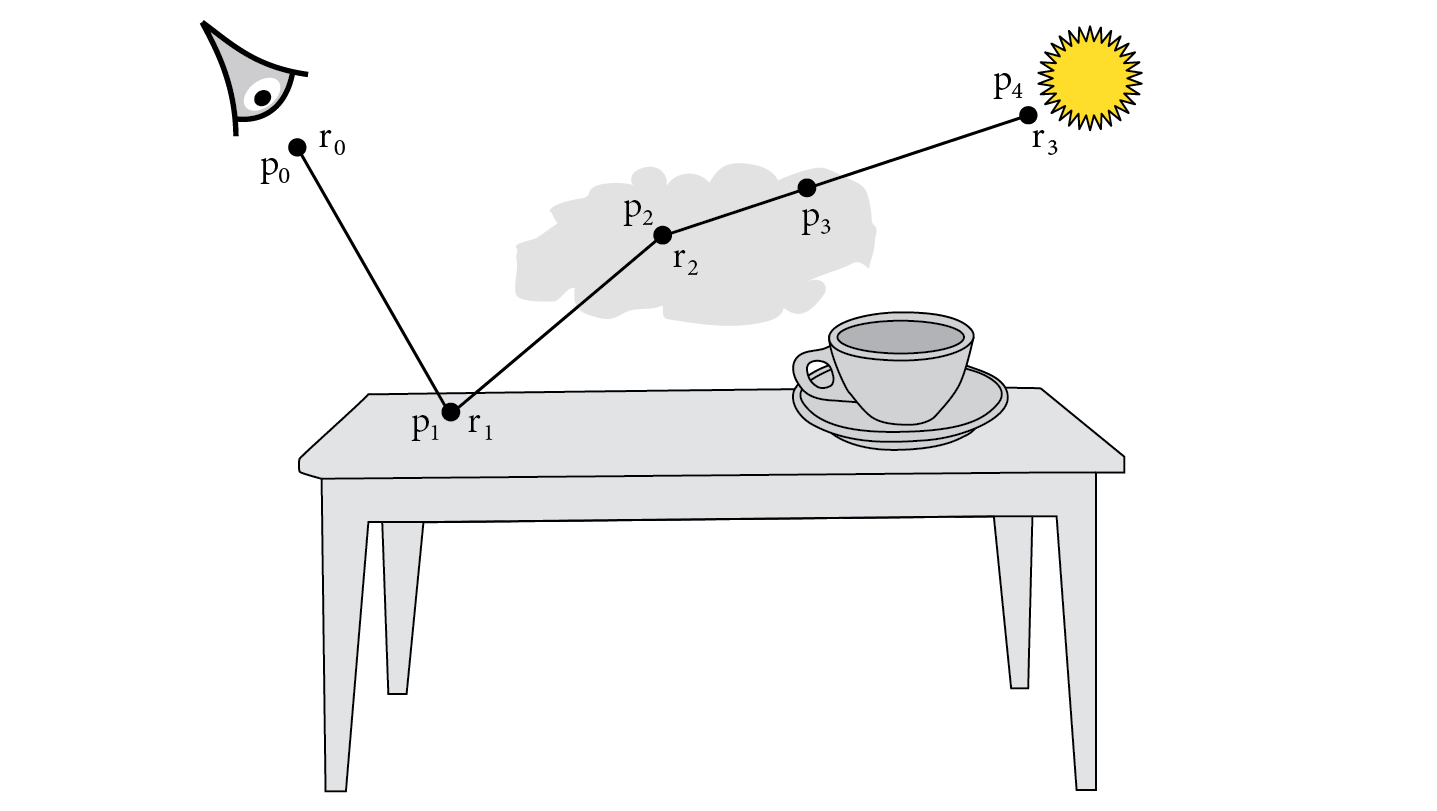
The path throughput function can then be defined as:
It now refers to a generalized scattering distribution function and generalized geometric term . The former simply falls back to the BSDF, phase function (multiplied by ), or a factor that enforces the ordering of null-scattering vertices, depending on the type of the vertex . Note that the first two products in Equation (14.11) are over all vertices but the third is only over real-scattering vertices.
The scattering distribution function is defined by
Here, is the Heaviside function, which is 1 if its parameter is positive and 0 otherwise.
Equation (13.2) in Section 13.1.3 originally defined the geometric term as
A generalized form of this geometric term is given by
where
incorporates the absolute angle cosine between the connection segment and the normal direction when the underlying vertex is located on a surface. Note that is only evaluated for real-scattering vertices , so the case of does not need to be considered.
Similar to integrating over the path space for surface scattering, the Monte Carlo estimator for the path contribution function can be defined for a path of path vertices . The resulting Monte Carlo estimator is
where is the probability of sampling the path with respect to the generalized path space measure.
Following Equation (13.8), we will also find it useful to define the volumetric path throughput weight
14.1.5 Evaluating the Volumetric Path Integral
The Monte Carlo estimator of the null-scattering path integral from Equation (14.14) allows sampling path vertices in a variety of ways; it is not necessary to sample them incrementally from the camera as in path tracing, for example. We will now reconsider sampling paths via path tracing under the path integral framework to show its use. For simplicity, we will consider scenes that have only volumetric scattering here.
The volumetric path-tracing algorithm from Section 14.1.2 is based on three sampling operations: sampling a distance along the current ray to a scattering event, choosing which type of interaction happens at that point, and then sampling a new direction from that point if the path has not been terminated. We can write the corresponding Monte Carlo estimator for the generalized path contribution function from Equation (14.14) with the path probability expressed as the product of three probabilities:
- : the probability of sampling the point along the direction from the point .
- : the discrete probability of sampling the type of scattering event—absorption, real-, or null-scattering—that was chosen at .
- : the probability of sampling the direction after a regular scattering event at point with incident direction .
For an vertex path with real-scattering vertices, the resulting estimator is
where denotes the direction from to and where the factor in the denominator accounts for the change of variables from sampling with respect to solid angle to sampling with respect to the path space measure.
We consider each of the three sampling operations in turn, starting with distance sampling, which has density . Assuming a single majorant , we find that has density , and the exponential factors cancel out the factors in , each one leaving behind a factor. Expanding out and simplifying, including eliminating the factors, all of which also cancel out, we have the estimator
Consider next the discrete choice among the three types of scattering event. The probabilities are all of the form , according to which type of scattering event was chosen at each vertex. The factor in Equation (14.17) cancels, leaving us with
The first factors must be either real or null scattering, and the last must be , given how the path was sampled. Thus, the estimator is equivalent to
Because we are for now neglecting surface scattering, represents either regular volumetric scattering or null scattering. Recall from Equation (14.12) that includes a or factor in those respective cases, which cancels out all the corresponding factors in the product in the denominator. Further, note that the Heaviside function for null scattering’s function is always 1 given how vertices are sampled with path tracing, so we can also restrict ourselves to the remaining real-scattering events in the numerator. Our estimator simplifies to