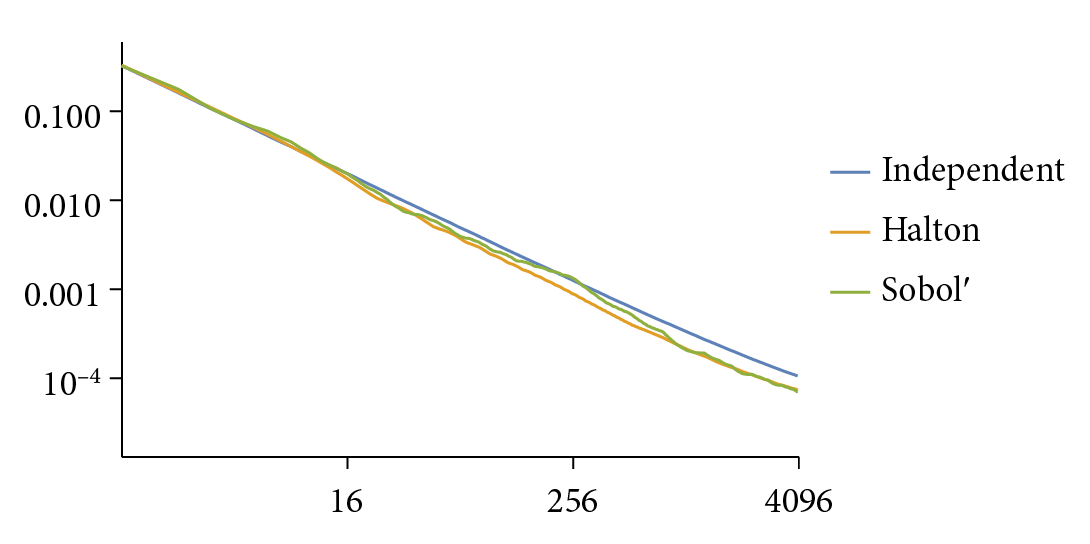8.7 Sobol’ Samplers

While the Halton sequence is effective for Monte Carlo integration, each radical inverse computation requires one integer division for each digit. The integer division instruction is one of the slowest ones on most processors, which can affect overall rendering performance, especially in highly optimized renderers. Therefore, in this section we will describe three Samplers that are based on the Sobol’ sequence, a low-discrepancy sequence that is defined entirely in base 2, which leads to efficient implementations.

The base-2 radical inverse can be computed more efficiently than the way that the base-agnostic RadicalInverse() function computes it. The key is to take advantage of the fact that numbers are already represented in base 2 on digital computers. If is a 64-bit value, then from Equation (8.18),

where are its bits. First, consider reversing its bits, still represented as an integer value, which gives

If we then divide this value by , we have

which equals (recall Equation (8.19)). Thus, the base-2 radical inverse can equivalently be computed using a bit reverse and a power-of-two division. The division can be replaced with multiplication by the corresponding inverse power-of-two, which gives the same result with IEEE floating point. Some processors provide a native instruction that directly reverses the bits in a register; otherwise it can be done in operations, where is the number of bits. (See the implementation of ReverseBits32() in Section B.2.7.)

While the implementation of a function that generates Halton points could be optimized by taking advantage of this for the first dimension where , performance would not improve for any of the remaining dimensions, so the overall benefit would be low. The Sobol’ sequence uses for all dimensions, which allows it to benefit in all cases from computers’ use of base 2 internally. So that each dimension has a different set of sample values, it uses a different generator matrix for each dimension, where the generator matrices are carefully chosen so that the resulting sequence has low discrepancy.

To see how generator matrices are used, consider an -digit number in base , where the th digit of is and where we have an generator matrix . Then the corresponding sample point is defined by

where all arithmetic is performed in the ring (in other words, when all operations are performed modulo ). This construction gives a total of points as ranges from to . If the generator matrix is the identity matrix, then this definition corresponds to the regular radical inverse, base . (It is worth pausing to make sure you see this connection between Equations (8.19) and (8.22) before continuing.)

In this section, we will exclusively use and . While introducing a matrix to each dimension of the sample generation algorithm may not seem like a step toward better performance, we will see that in the end the sampling code can be mapped to an implementation that uses a small number of bit operations that perform this computation in an extremely efficient manner.

The first step toward high performance comes from the fact that we are working in base 2; as such, all entries of are either 0 or 1 and thus we can represent either each row or each column of the matrix with a single unsigned 32-bit integer. We will choose to represent columns of the matrix as uint32_ts; this choice leads to an efficient algorithm for multiplying the column vector by .

Now consider the task of computing the matrix-vector product; using the definition of matrix-vector multiplication, we have:

In other words, for each digit of that has a value of 1, the corresponding column of should be summed. This addition can in turn be performed efficiently in : in that setting, addition corresponds to the bitwise exclusive or operation. (Consider the combinations of the two possible operand values—0 and 1—and the result of adding them , and compare to the values computed by exclusive or with the same operand values.) Thus, the multiplication is just a matter of exclusive oring together the columns of where ’s bit is 1. This computation is implemented in the MultiplyGenerator() function.

Going back to Equation (8.22), if we denote the column vector from the product , then consider the vector product

Applying the same ideas as we did before to derive an efficient base-2 radical inverse algorithm, this value can also be computed by reversing the bits of and dividing by . To save the small cost of reversing the bits, we can equivalently reverse the bits in all the columns of the generator matrix before passing it to MultiplyGenerator(). We will use that convention in what follows.

We will not discuss how the Sobol’ matrices are derived in a way that leads to a low-discrepancy sequence; the “Further Reading” section has pointers to more details. However, the first few Sobol’ generator matrices are shown in Figure 8.34. Note that the first is the identity, corresponding to the van der Corput sequence. Subsequent dimensions have various fractal-like structures to their entries.

8.7.1 Stratification over Elementary Intervals

The first two dimensions of the Sobol’ sequence are stratified in a very general way that makes them particularly effective in integration. For example, the first 16 samples satisfy the stratification constraint from stratified sampling in Section 8.5, meaning there is just one sample in each of the boxes of extent . However, they are also stratified over all the boxes of extent and . Furthermore, there is only one sample in each of the boxes of extent and . Figure 8.35 shows all the possibilities for dividing the domain into regions where the first 16 Sobol’ samples satisfy these stratification properties.

Not only are corresponding stratification constraints obeyed by any power-of-2 set of samples starting from the beginning of the sequence, but subsequent power-of-2-sized sets of samples fulfill them as well. More formally, any sequence of length (where is a nonnegative integer) satisfies this general stratification constraint. The set of elementary intervals in two dimensions, base 2, is defined as

where the integer . One sample from each of the first values in the sequence will be in each of the elementary intervals. Furthermore, the same property is true for each subsequent set of values. Such a sequence is called a -sequence.

8.7.2 Randomization and Scrambling

For the same reasons as were discussed in Section 8.6.2 in the context of the Halton sequence, it is also useful to be able to scramble the Sobol’ sequence. We will now define a few small classes that scramble a given sample value using various approaches. As with the generation of Sobol’ samples, scrambling algorithms for them can also take advantage of their base-2 representation to improve their efficiency.

All the following randomization classes take an unsigned 32-bit integer that they should interpret as a fixed-point number with 0 digits before and 32 digits after the radix point. Put another way, after randomization, this value will be divided by to yield the final sample value in .

The simplest approach is not to randomize the sample at all. In that case, the value is returned unchanged; this is implemented by NoRandomizer.

Alternatively, random permutations can be applied to the digits, such as was done using the DigitPermutation class with the Halton sampler. In base 2, however, a random permutation of can be represented with a single bit, as there are only two unique permutations. If the permutation is denoted by a bit with value 1 and the permutation is denoted by 0, then the permutation can be applied by computing the exclusive or of the permutation bit with a digit’s bit. Therefore, the permutation for all 32 bits can be represented by a 32-bit integer and all of the permutations can be applied in a single operation by computing the exclusive or of the provided value with the permutation.

Owen scrambling is also effective with Sobol’ points. pbrt provides two implementations of it, both of which take advantage of their base-2 representation. FastOwenScrambler implements a highly efficient approach, though the spectral properties of the resulting points are not quite as good as a true Owen scramble.

Its implementation builds on the fact that in base 2, if a number is multiplied by an even value, then the value of any particular bit in it only affects the bits above it in the result. Equivalently, for any bit in the result, it is only affected by the bits below it and the even multiplicand. One way to see why this is so is to consider long multiplication (as taught in grade school) applied to binary numbers. Given two -digit binary numbers and where is the th digit of , then using Equation (8.18), we have

Thus, for any digit where is one, the value of is shifted bits to the left and added to the final result and so any digit of the result only depends on lower digits of .

The bits in the value provided to the randomization class must be reversed so that the low bit corresponds to in the final sample value. Then, the properties illustrated in Equation (8.25) can be applied: the product of an even value with the sample value v can be interpreted as a bitwise permutation as was done in the BinaryPermuteScrambler, allowing the use of an exclusive or to permute all the bits. After a few rounds of this and a few operations to mix the seed value in, the bits are reversed again before being returned.

The OwenScrambler class implements a full Owen scramble, operating on each bit in turn.

The first bit (corresponding to in the final sample value) is handled specially, since there are no bits that precede it to affect its randomization. It is randomly flipped according to the seed value provided to the constructor.

For all the following bits, a bit mask is computed such that the bitwise and of the mask with the value gives the bits above b—the values of which should determine the permutation that is used for the current bit. Those are run through MixBits() to get a hashed value that is then used to determine whether or not to flip the current bit.

8.7.3 Sobol’ Sample Generation

We now have the pieces needed to implement functions that generate Sobol’ samples. The SobolSample() function performs this task for a given sample index a and dimension, applying the provided randomizer to the sample before returning it.

Because this function is templated on the type of the randomizer, a specialized instance of it will be compiled using the provided randomizer, leading to the randomization algorithm being expanded inline in the function. For pbrt’s purposes, there is no need for a more general mechanism for sample randomization, so the small performance benefit is worth taking in this implementation approach.

Samples are computed using the Sobol’ generator matrices, following the approach described by Equation (8.23). All the generator matrices are stored consecutively in the SobolMatrices32 array. Each one has SobolMatrixSize columns, so scaling the dimension by SobolMatrixSize brings us to the first column of the matrix for the given dimension.

The value is then randomized with the given randomizer before being rescaled to . (The constant 0x1p-32 is , expressed as a hexadecimal floating-point number.)

8.7.4 Global Sobol’ Sampler

The SobolSampler generates samples by direct evaluation of the -dimensional Sobol’ sequence. Like the HaltonSampler, it scales the first two dimensions of the sequence to cover a range of image pixels. Thus, in a similar fashion, nearby pixels have well-distributed -dimensional sample points not just individually but also with respect to nearby pixels.

The SobolSampler uniformly scales the first two dimensions by the smallest power of 2 that causes the sample domain to cover the image area to be sampled. As with the HaltonSampler, this specific scaling scheme is chosen in order to make it easier to compute the reverse mapping from pixel coordinates to the sample indices that land in each pixel.

All four of the randomization approaches from Section 8.7.2 are supported by the SobolSampler; randomize encodes which one to apply.

The sampler needs to record the current pixel for use in its GetPixel2D() method and, like other samplers, tracks the current dimension in its dimension member variable.

The SobolIntervalToIndex() function returns the index of the sampleIndexth sample in the pixel p, if the sampling domain has been scaled by to cover the pixel sampling area.

The general approach used to derive the algorithm it implements is similar to that used by the Halton sampler in its StartPixelSample() method. Here, scaling by a power of two means that the base-2 logarithm of the scale gives the number of digits of the product that form the scaled sample’s integer component. To find the values of that give a particular integer value after scaling, we can compute the inverse of : given

then equivalently

We will not include the implementation of this function here.

Sample generation is now straightforward. There is the usual management of the dimension value, again with the first two dimensions reserved for the pixel sample, and then a call to SampleDimension() gives the sample for a single Sobol’ dimension.

The SampleDimension() method takes care of calling SobolSample() for the current sample index and specified dimension using the appropriate randomizer.

If a randomizer is being used, a seed value must be computed for it. Note that the hash value passed to each randomizer is based solely on the current dimension and user-provided seed, if any. It must not be based on the current pixel or the current sample index within the pixel, since the same randomization should be used at all the pixels and all the samples within them.

2D sample generation is easily implemented using SampleDimension(). If all sample dimensions have been consumed, Get2D() goes back to the start and skips the first two dimensions, as was done in the HaltonSampler.

Pixel samples are generated using the first two dimensions of the Sobol’ sample. SobolIntervalToIndex() does not account for randomization, so the NoRandomizer is always used for the pixel sample, regardless of the value of randomize.

The samples returned for the pixel position need to be adjusted so that they are offsets within the current pixel. Similar to what was done in the HaltonSampler, the sample value is scaled so that the pixel coordinates are in the integer component of the result. The remaining fractional component gives the offset within the pixel that the sampler returns.

8.7.5 Padded Sobol’ Sampler

The SobolSampler generates sample points that have low discrepancy over all of their dimensions. However, the distribution of samples in two-dimensional slices of the - dimensional space is not necessarily particularly good. Figure 8.36 shows an example.

For rendering, this state of affairs means that, for example, the samples taken over the surface of a light source at a given pixel may not be well distributed. It is of only slight solace to know that the full set of -dimensional samples are well distributed in return. Figure 8.37 shows this problem in practice with the SobolSampler: 2D projections of the form shown in Figure 8.36 end up generating a characteristic checkerboard pattern in the image at low sampling rates.

Therefore, the PaddedSobolSampler generates samples from the Sobol’ sequence in a way that focuses on returning good distributions for the dimensions used by each 1D and 2D sample independently. It does so via padding samples, similarly to the StratifiedSampler, but here using Sobol’ samples rather than jittered samples.

The constructor, not included here, initializes the following member variables from provided values. As with the SobolSampler, using a pixel sample count that is not a power of 2 will give suboptimal results; a warning is issued in this case.

StartPixelSample(), also not included here, just records the specified pixel, sample index, and dimension.

1D samples are generated by randomly shuffling a randomized van der Corput sequence.

Here, the permutation used for padding is based on the current pixel and dimension. It must not be based on the sample index, as the same permutation should be applied to all sample indices of a given dimension in a given pixel.

Given the permuted sample index value index, a separate method, SampleDimension(), takes care of generating the corresponding Sobol’ sample. The high bits of the hash value are reused for the sample’s randomization; doing so should be safe, since PermutationElement() uses the hash it is passed in an entirely different way than any of the sample randomization schemes do.

SampleDimension() follows the same approach as the corresponding method in SobolSampler, creating the appropriate randomizer before calling SobolSample().

Padded 2D samples are generated starting with a similar permutation of sample indices.

Randomization also parallels the 1D case; again, bits from hash are used both for the random permutation of sample indices and for sample randomization.

For this sampler, pixel samples are generated in the same manner as all other 2D samples, so the sample generation request is forwarded on to Get2D().

8.7.6 Blue Noise Sobol’ Sampler

ZSobolSampler is a third sampler based on the Sobol’ sequence. It is also based on padding 1D and 2D Sobol’ samples, but uses sample indices in a way that leads to a blue noise distribution of sample values. This tends to push error to higher frequencies, which in turn makes it appear more visually pleasing. Figure 8.38 compares a scene rendered with the PaddedSobolSampler and the ZSobolSampler; both have essentially the same MSE, but the one rendered using ZSobolSampler looks better to most human observers. This Sampler is the default one used by pbrt if no sampler is specified in the scene description.

This sampler generates blue noise samples by taking advantage of the properties of -sequences. To understand the idea behind its implementation, first consider rendering a two-pixel image using 16 samples per pixel where a set of 2D samples are used for area light source sampling in each pixel. If the first 16 samples from a -sequence are used for the first pixel and the next 16 for the second, then not only will each pixel individually use well-stratified samples, but the set of all 32 samples will collectively be well stratified thanks to the stratification of -sequences over elementary intervals (Section 8.7.1). Consequently, the samples used in each pixel will generally be in different locations than in the other pixel, which is precisely the sample decorrelation exhibited by blue noise. (See Figure 8.39.)

More generally, if all the pixels in an image take different power-of-2 aligned and sized segments of samples from a single large set of Sobol’ samples in a way that nearby pixels generally take adjacent segments, then the distribution of samples across the entire image will be such that pixels generally use different sample values than their neighbors. Allocating segments of samples in scanline order would give good distributions along scanlines, but it would not do much from scanline to scanline. The Morton curve, which was introduced earlier in Section 7.3.3 in the context of linear bounding volume hierarchies, gives a better mechanism for this task: if we compute the Morton code for each pixel and then use that to determine the pixel’s starting index into the full set of Sobol’ samples, then nearby pixels—those that are nearby in both and —will tend to use nearby segments of the samples. This idea is illustrated in Figure 8.40.

Used directly in this manner, the Morton curve can lead to visible structure in the image; see Figure 8.41, where samples were allocated in that way. This issue can be addressed with a random permutation of the Morton indices interpreted as base-4 numbers, which effectively groups pairs of one bit from and one bit from in the Morton index into single base-4 digits. Randomly permuting these digits still maintains much of the spatial coherence of the Morton curve; see Figure 8.42 for an illustration of the permutation approach. Figure 8.38(b) shows the resulting improvement in a rendered image.

A second problem with the approach as described so far is that it does not randomize the order of sample indices within a pixel, as is necessary for padding samples across different dimensions. This shortcoming can be addressed by appending the bits of the sample index within a pixel to the pixel’s Morton code and then including those in the index randomization as well.

In addition to the usual configuration parameters, the ZSobolSampler constructor also stores the base-2 logarithm of the number of samples per pixel as well as the number of base-4 digits in the full extended Morton index that includes the sample index.

The StartPixelSample() method’s main task is to construct the initial unpermuted sample index by computing the pixel’s Morton code and then appending the sample index, using a left shift to make space for it. This value is stored in mortonIndex.

Sample generation is similar to the PaddedSobolSampler with the exception that the index of the sample is found with a call to the GetSampleIndex() method (shown next), which randomizes mortonIndex. The <<Generate 1D Sobol sample at sampleIndex>> fragment then calls SobolSample() to generate the sampleIndexth sample using the appropriate randomizer. It is otherwise effectively the same as the PaddedSobolSampler::SampleDimension() method, so its implementation is not included here.

2D samples are generated in a similar manner, using the first two Sobol’ sequence dimensions and a sample index returned by GetSampleIndex(). Here as well, the fragment that dispatches calls to SobolSample() corresponding to the chosen randomization scheme is not included.

Pixel samples are generated the same way as other 2D sample distributions.

The GetSampleIndex() method is where most of the complexity of this sampler lies. It computes a random permutation of the digits of mortonIndex, including handling the case where the number of samples per pixel is only a power of 2 but not a power of 4; that case needs special treatment since the total number of bits in the index is odd, which means that only one of the two bits needed for the last base-4 digit is available.

We will find it useful to have all of the permutations of four elements explicitly enumerated; they are stored in the permutations array.

The digits are randomized from most significant to least significant. In the case of the number of samples only being a power of 2, the loop terminates before the last bit, which is handled specially since it is not a full base-4 digit.

After the current digit is extracted from mortonIndex, it is permuted using the selected permutation before being shifted back into place to be added to sampleIndex.

Which permutation to use is determined by hashing both the higher-order digits and the current sample dimension. In this way, the index is hashed differently for different dimensions, which randomizes the association of samples in different dimensions for padding. The use of the higher-order digits in this way means that this approach bears some resemblance to Owen scrambling, though here it is applied to sample indices rather than sample values. The result is a top-down hierarchical randomization of the Morton curve.

In the case of a power-of-2 sample count, the single remaining bit in mortonIndex is handled specially, though following the same approach as the other digits: the higher-order bits and dimension are hashed to choose a permutation. In this case, there are only two possible permutations, and as with the BinaryPermuteScrambler, an exclusive or is sufficient to apply whichever of them was selected.

8.7.7 Evaluation

In this section we have defined three Samplers, each of which supports four randomization algorithms, giving a total of 12 different ways of generating samples. All are effective samplers, though their characteristics vary. In the interest of space, we will not include evaluations of every one of them here but will focus on the most significant differences among them.

Figure 8.43(a) shows the PSD of the unscrambled 2D Sobol’ point set; it is an especially bad power spectrum. Like the Halton points, the 2D Sobol’ points have low energy along the two axes thanks to well-distributed 1D projections, but there is significant structured variation at higher off-axis frequencies, including regions with very high PSD values. As seen in Figure 8.43(b), randomizing the Sobol’ points with random digit permutations only slightly improves the power spectrum. Only with the Owen scrambling algorithms does the power spectrum start to become uniform at higher frequencies, though some structure still remains (Figures 8.43(c) and (d)).

These well-distributed 1D projections are one reason why low-discrepancy sequences are generally more effective than stratified patterns: they are more robust with respect to preserving their good distribution properties after being transformed to other domains. Figure 8.44 shows what happens when a set of 16 sample points are transformed to be points on a skinny quadrilateral by scaling them to cover its surface; samples from the Sobol’ sequence remain well distributed, but samples from a stratified pattern fare worse.

Returning to the simple scene with defocus blur that was used in Figure 8.23, Figure 8.45 compares using the Halton sampler to the three Sobol’ samplers for rendering that scene. We can see that the Halton sampler has higher error than the StratifiedSampler, which is due to its 2D projections (as are used for sampling the lens) not necessarily being well distributed. The PaddedSobolSampler gives little benefit over the stratified sampler, since for sampling a lens, the stratification is the most important one and both fulfill that. The SobolSampler has remarkably low error, even though the rendered image shows the characteristic structure of 2D projections of the Sobol’ sequence. The ZSobolSampler combines reasonably low error with the visual benefit of distributing its error with blue noise.

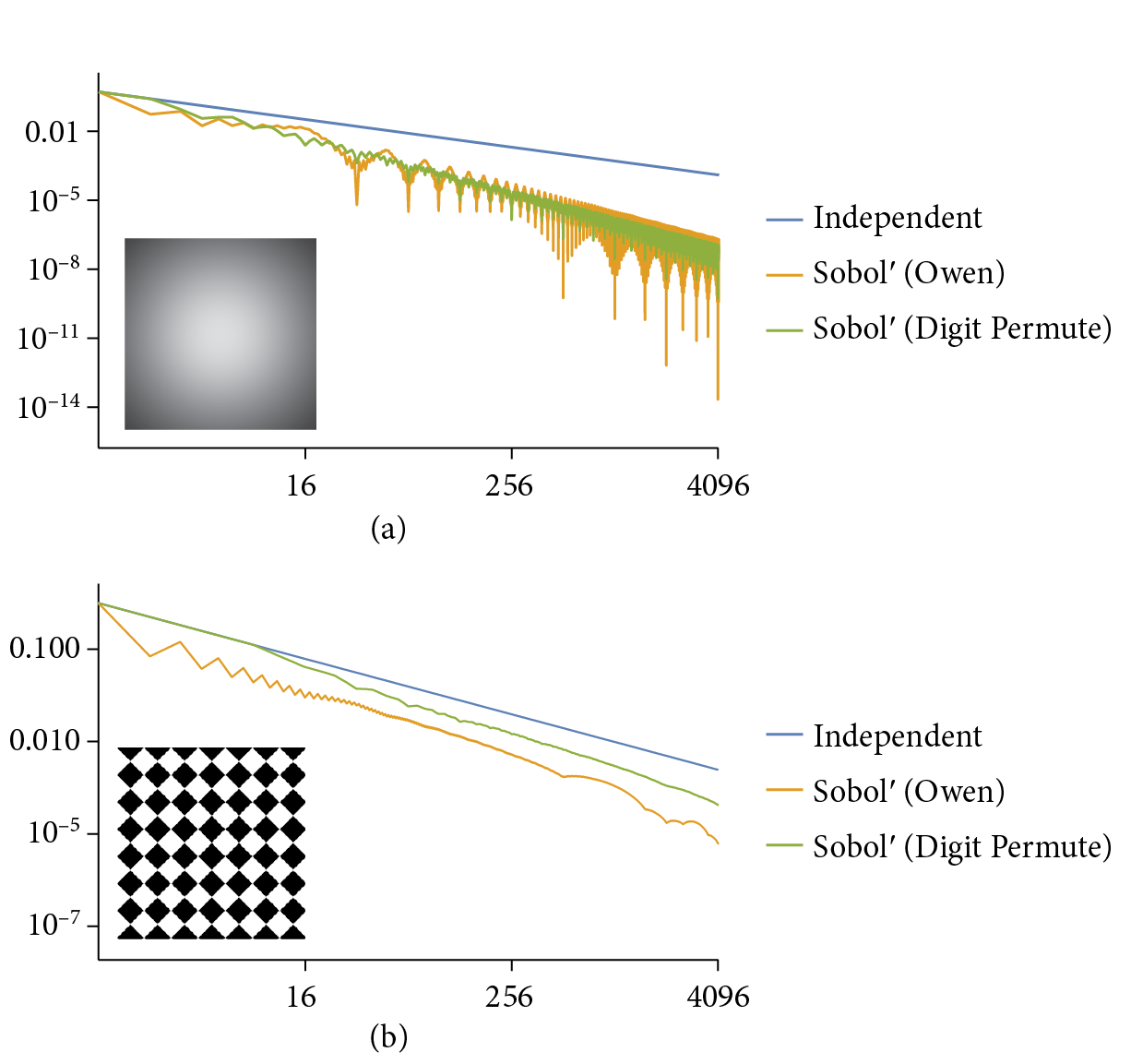
Figure 8.46 shows the performance of Sobol’ sample points with the two test functions. It does well with both, but especially so with Owen scrambled points and the smooth Gaussian function, where it has an asymptotically faster rate of convergence. Figure 8.47 graphs MSE versus the sample count for the blurry dragon test scene from Figure 8.32. Both the Halton and Sobol’ samplers have roughly 10% lower MSE than independent sampling at equivalent sample counts.