15.2 Implementation Foundations
Before we discuss the implementation of the wavefront integrator and the details of its kernels, we will start by discussing some of the lower-level capabilities that it is built upon, as well as the abstractions that we use to hide the details of platform-specific APIs.
15.2.1 Execution and Memory Space Specification
If you have perused the pbrt source code, you will have noticed that the signatures of many functions include a PBRT_CPU_GPU. We have elided all of these from the book text thus far in the interests of avoiding distraction. Now we must pay closer attention to them.
When pbrt is compiled with GPU support, the compiler must know whether each function in the system is intended for CPU execution only, GPU execution only, or execution on both types of processor. In some cases, a function may only be able to run on one of the two—for example, if it uses low-level functionality that the other type of processor does not support. In other cases, it may be possible for it to run on both, though it may not make sense to do so. For example, an object constructor that does extensive serial processing would be unsuited to the GPU.
PBRT_CPU_GPU hides the platform-specific details of how these characteristics are indicated. (With CUDA, it turns into a __host__ __device__ specifier.) There is also a PBRT_GPU macro, which signifies that a function can only be called from GPU code. These macros are all defined in the file pbrt.h. If no specifier is provided, a function can only be called from code that is running on the CPU.
These specifiers can be used with variable declarations as well, to similar effect. pbrt only makes occasional use of them for that, mostly using managed memory for such purposes. (There is also a PBRT_CONST variable qualifier that is used to define large constant arrays in a way that makes them accessible from both CPU and GPU.)
In addition to informing the compiler of which processors to compile functions for, having these specifiers in the signatures of functions allows the compiler to determine whether a function call is valid: a CPU-only function that directly calls a GPU-only function, or vice versa, leads to a compile time error.
15.2.2 Launching Kernels on the GPU
pbrt also provides functions that abstract the platform-specific details of launching kernels on the GPU. These are all defined in the files gpu/util.h and gpu/util.cpp.
The most important of them is GPUParallelFor(), which launches a specified number of GPU threads and invokes the provided kernel function for each one, passing it an index ranging from zero up to the total number of threads. The index values passed always span a contiguous range for all of the threads in a thread group. This is an important property in that, for example, indexing into a float array using the index leads to contiguous memory accesses.
This function is the GPU analog to ParallelFor(), with the differences that it always starts iteration from zero, rather than taking a 1D range, and that it takes a description string that describes the kernel’s functionality. Its implementation includes code that tracks the total time each kernel spends executing on the GPU, which makes it possible to print a performance breakdown after rendering completes using the provided description string.
Similar to ParallelFor(), all the work from one call to GPUParallelFor() finishes before any work from a subsequent call to GPUParallelFor() begins, and it, too, is also generally used with lambda functions. A simple example of its usage is below: the callback function func is invoked with a single integer argument, corresponding to the item index that it is responsible for. Note also that a PBRT_GPU specifier is necessary for the lambda function to indicate that it will be invoked from GPU code.
We provide a macro for specifying lambda functions for GPUParallelFor() and related functions that adds the PBRT_GPU specifier and also hides some platform-system specific details (which are not included in the text here).
We do not provide a variant analogous to ParallelFor2D() for iterating over a 2D array, though it would be easy to do so; pbrt just has no need for such functionality.
Although execution is serialized between successive calls to GPUParallelFor(), it is important to be aware that the execution of the CPU and GPU are decoupled. When a call to GPUParallelFor() returns on the CPU, the corresponding threads on the GPU often will not even have been launched, let alone completed. Work on the GPU proceeds asynchronously. While this execution model thus requires explicit synchronization operations between the two processors, it is important for achieving high performance. Consider the two alternatives illustrated in Figure 15.3; automatically synchronizing execution of the two processors would mean that only one of them could be running at a given time.
An implication of this model is that the CPU must be careful about when it reads values from managed memory that were computed on the GPU. For example, if the implementation had code that tried to read the final image immediately after launching the last rendering kernel, it would almost certainly read an incomplete result. We therefore require a mechanism so that the CPU can wait for all the previous kernel launches to complete. This capability is provided by GPUWait(). Again, the implementation is not included here, as it is based on platform-specific functionality.
15.2.3 Structure-of-Arrays Layout
As discussed earlier, the thread group execution model of GPUs affects the pattern of memory accesses that program execution generates. A consequence is that the way in which data is laid out in memory can have a meaningful effect on performance. To understand the issue, consider the following definition of a ray structure:
Now consider a kernel that takes a queue of SimpleRays as input. Such a kernel might be responsible for finding the closest intersection along each ray, for example. A natural representation of the queue would be an array of SimpleRays. (This layout is termed array of structures, and is sometimes abbreviated as AOS.) Such a queue would be laid out in memory as shown in Figure 15.4, where each SimpleRay occupies a contiguous region of memory with its elements stored in consecutive locations in memory.
Now consider what happens when the threads in a thread group read their corresponding ray into memory. If the pointer to the array is rays and the index passed to each thread’s lambda function is i, then each thread might start out by reading its ray using code like
The generated code would typically load each component of the origins and directions individually. Figure 15.5(a) illustrates the distribution of memory locations accessed when each thread in a thread group loads the x component of its ray origin. The locations span many cache lines, which in turn incurs a performance cost.
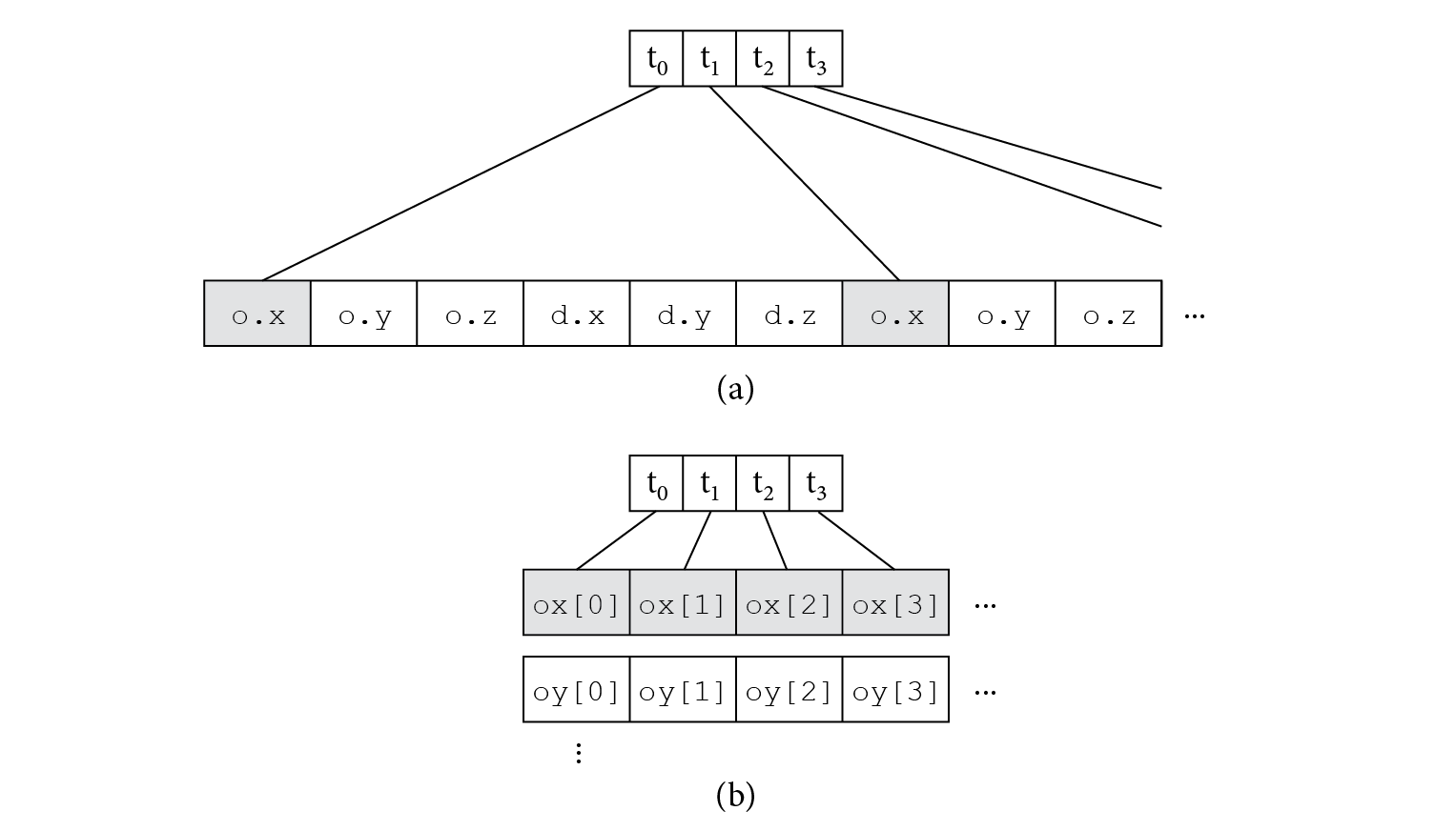
An alternative layout is termed structure of arrays, or SOA. The idea behind this approach is to effectively transpose the layout of the object in memory, storing all the origins’ x components contiguously in an array of Floats, then all of its origins’ y components in another Float array, and so forth. We might declare a specialized structure to represent arrays of SimpleRays laid out like this:
In turn, if the threads in a thread group want to load the x component of their ray’s origin, the expression rays.ox[i] suffices to load that value. The locations accessed are contiguous in memory and span many fewer cache lines (Figure 15.5(b)).
However, this performance benefit comes at a cost of making the code more unwieldy. Loading an entire ray with this approach requires indexing into each of the constituent arrays—for example,
Even more verbose manual indexing is required for the task of writing a ray out to memory in SOA format; the cleanliness of the AOS array syntax has been lost.
In order to avoid such complexity, the code in the remainder of this chapter makes extensive use of SOA template types that make it possible to work with SOA data using syntax that is the same as array indexing with an array of structures data layout. For any type that has an SOA template specialization (e.g., pbrt’s regular Ray class), we are able to write code like the following:
Both loads from and stores to the array are expressed using regular C++ array indexing syntax.
While it is straightforward programming to implement such SOA classes, doing so is rather tedious, especially if one has many types to lay out in SOA. Therefore, pbrt includes a small utility program, soac (structure of arrays compiler), that automates this process. Its source code is in the file cmd/soac.cpp in the pbrt distribution. There is not much to be proud of in its implementation, so we will not discuss that here, but we will describe its usage as well as the form of the SOA type definitions that it generates.
soac takes structure specifications in a custom format of the following form:
Here, flat specifies that the following type should be stored directly in arrays, while soa specifies a structure. Although not shown here, soa structures can themselves hold other soa structure types. See the files pbrt.soa and wavefront/workitems.soa in the pbrt source code for more examples.
This format is easy to parse and is sufficient to provide the information necessary to generate pbrt’s SOA type definitions. A more bulletproof solution (and one that would avoid the need for writing the code to parse a custom format) would be to modify a C++ compiler to optionally emit SOA type definitions for types it has already parsed. Of course, that is a more complex approach to implement than soac was.
When pbrt is compiled, soac is invoked to generate header files based on the *.soa specifications. For example, pbrt.soa is turned into pbrt_soa.h, which can be found in pbrt’s build directory after the system has been compiled. For each soa type defined in a specification file, soac generates an SOA template specialization. Here is the one for Point2f. (Here we have taken automatically generated code and brought it into the book text for dissection, which is the opposite flow from all the other code in the text.)
The constructor uses a provided allocator to allocate space for individual arrays for the class member variables. The use of the this-> syntax for initializing the member variables may seem gratuitous, though it ensures that if one of the member variables has the same name as one of the constructor parameters, it is still initialized correctly.
The SOA class’s members store the array size and the individual member pointers. The PBRT_RESTRICT qualifier informs the compiler that no other pointer will point to these arrays, which can allow it to generate more efficient code.
It is easy to generate a method that allows indexing into the SOA arrays to read values. Note that the generated code requires that the class has a default constructor and that it can directly initialize the class’s member variables. In the event that they are private, the class should use a friend declaration to make them available to its SOA specialization.
It is less obvious how to support assignment of values using the regular array indexing syntax. soac provides this capability through the indirection of an auxiliary class, GetSetIndirector. When operator[] is called with a non-const SOA object, it returns an instance of that class. It records not only a pointer to the SOA object but also the index value.
Assignment is handled by the GetSetIndirector’s operator= method. Given a Point2f value, it is able to perform the appropriate assignments using the SOA * and the index.
Variables of type GetSetIndirector should never be declared explicitly. Rather, the role of this structure is to cause an assignment of the form p[i] = Point2f(...) to correspond to the following code, where the initial parenthesized expression corresponds to invoking the SOA class’s operator[] to get a temporary GetSetIndirector and where the assignment is then handled by its operator= method.
GetSetIndirector also provides an operator Point2f() conversion operator (not included here) that handles the case of an SOA array read with a non-const SOA object.
We conclude with a caveat: SOA layout is effective if access is coherent, but can be detrimental if it is not. If threads are accessing an array of some structure type in an incoherent fashion, then AOS may be a better choice: in that case, although each thread’s initial access to the structure may incur a cache miss, its subsequent accesses may be efficient if nearby values in the structure are still in the cache. Conversely, incoherent access to SOA data may incur a miss for each access to each structure member, polluting the cache by bringing in many unnecessary values that are not accessed by any other threads.
15.2.4 Work Queues
Our last bit of groundwork before getting back into rendering will be to define two classes that manage the input and output of kernels in the ray-tracing pipeline. Both are defined in the file wavefront/workqueue.h.
First is WorkQueue, which represents a queue of objects of a specified type, WorkItem. The items in the queue are stored in SOA layout; this is achieved by publicly inheriting from the SOA template class for the item type. This inheritance also allows the items in the work queue to be indexed using regular array indexing syntax, via the SOA public methods.
The constructor takes the maximum number of objects that can be stored in the queue as well as an allocator, but leaves the actual allocation to the SOA base class.
There is only a single private member variable: the number of objects stored in the queue. It is represented using a platform-specific atomic type. When WorkQueues are used on the CPU, a std::atomic is sufficient; that case is shown here.
Simple methods return the size of the queue and reset it so that it stores no items.
An item is added to the queue by finding a slot for it via a call to AllocateEntry(). We implement that functionality separately so that WorkQueue subclasses can implement their own methods for adding items to the queue if further processing is needed when doing so. In this case, all that needs to be done is to store the provided value in the specified spot using the SOA indexing operator.
When a slot is claimed for a new item in the queue, the size member variable is incremented using an atomic operation, and so it is fine if multiple threads are concurrently adding items to the queue without any further coordination.
Returning to how threads access memory, we would do well to allocate consecutive slots for all of the threads in a thread group that are adding entries to a queue. Given the SOA layout of the queue, such an allocation leads to writes to consecutive memory locations, with corresponding performance benefits. Our use of fetch_add here does not provide that guarantee, since each thread calls it independently. However, a common way to implement atomic addition in the presence of thread groups is to aggregate the operation over all the active threads in the group and to perform a single addition for all of them, doling out corresponding individual results back to the individual threads. Our code here assumes such an implementation; on a platform where the assumption is incorrect, it would be worthwhile to use a different mechanism that did give that result.
ForAllQueued() makes it easy to apply a function to all of the items stored in a WorkQueue() in parallel. The provided callback function is passed the WorkItem that it is responsible for.
If the GPU is being used, a thread is launched for the maximum number of items that could be stored in the queue, rather than only for the number that are actually stored there. This stems from the fact that kernels are launched from the CPU but the number of objects actually in the queue is stored in managed memory. Not only would it be inefficient to read the actual size of the queue back from GPU memory to the CPU for the call to GPUParallelFor(), but retrieving the correct value would require synchronization with the GPU, which would further harm performance.
Therefore, a number of threads certain to be sufficient are launched and those that do not have an item to process exit immediately. Because thread creation is so inexpensive on GPUs, this approach does not introduce a meaningful amount of overhead. If it was a problem, it is also possible to launch kernels directly from the GPU, in which case exactly the correct number of threads could be launched. In this case, we adopt the greater simplicity of always launching kernels from the CPU.
For CPU processing, there are no concerns about reading the size field, so precisely the right number of items to process can be passed to ParallelFor().
We will also find it useful to have work queues that support multiple types of objects and maintain separate queues, one for each type. This functionality is provided by the MultiWorkQueue.
The definition of this class is a variadic template specialization that takes all of the types Ts it is to manage using a TypePack.
The MultiWorkQueue internally expands to a set of per-type WorkQueue instances that are stored in a tuple.
Note the ellipsis (...) in the code fragment above, which is a C++ template pack expansion. Such an expansion is only valid when it contains a template pack (Ts in this case), and it simply inserts the preceding element once for each specified template argument while replacing Ts with the corresponding type. For example, a hypothetical MultiWorkQueue<TypePack<A, B>> would contain a tuple of the form pstd::tuple<WorkQueue<A>, WorkQueue<B>>. This and the following template-based transformations significantly reduce the amount of repetitive code that would otherwise be needed to implement equivalent functionality.
The following template method returns a queue for a particular work item that must be one of the MultiWorkQueue template arguments. The search through tuple items is resolved at compile time and so incurs no additional runtime cost.
The MultiWorkQueue constructor takes the maximum number of items to store in the queue and an allocator. The third argument is a span of Boolean values that indicates whether each type is actually present. Saving memory for types that are not required in a given execution of the renderer is worthwhile when both the maximum number of items is large and the work item types themselves are large.
Once more, note the use of the ellipsis in the above fragment, which is a more advanced case of a template pack expansion following the pattern ((expr), ...). As before, this expansion will simply repeat the element (expr) preceding the ellipsis once for every Ts with appropriate substitutions. In contrast to the previous case, we are now expanding expressions rather than types. The actual values of these expressions are ignored because they will be joined by the comma operator that ignores the value of the preceding expression. Finally, the actual expression being repeated has side effects: it initializes each tuple entry with a suitable instance, and it also advances a counter index that is used to access corresponding elements of the haveType span.
The Size() method returns the size of a queue, and Push() appends an element. Both methods require that the caller specify the concrete type T of work item, which allows it to directly call the corresponding method of the appropriate queue.
Finally, all queues are reset via a call to Reset(). Once again, template pack expansion generates calls to all the individual queues’ Reset() methods via the following terse code.